Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Функция y = x имеет следующий график:

Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Скачать домашнее задание к уроку 5.
Графики функций — ГИА В3
Здравствуйте, уважаемый посетитель! В этой статье будут разобраны задания В3 из ГИА, те, что связаны с графиками функций. Мы научимся определять все коэффициенты параболы по графику, находить точки пересечения прямой с осями координат и ее коэффициент наклона, а также ближе познакомимся с гиперболой.
Давайте начнем разбор этих заданий со знакомства с прямой и ее уравнением.
Прямая задается уравнением:  . В этом уравнении коэффициент k отвечает за наклон прямой, а коэффициент b – за смещение по оси y вверх или вниз.
. В этом уравнении коэффициент k отвечает за наклон прямой, а коэффициент b – за смещение по оси y вверх или вниз.

Уравнение прямой и его коэффициенты
И тот, и другой коэффициенты могут быть как положительными, так и отрицательными. В случае с коэффициентом b все понятно: [stextbox id=”alert” bwidth=”1″ bcolor=”5e56a9″ bgcolor=”0cb2f2″]если он положительный, то прямая пересекает ось y выше оси х, а если отрицательный – то ниже[/stextbox]. На рисунке этот коэффициент равен 2 для красной прямой (
 , для розовой –
, для розовой – 

Прямые с различными значениями коэффициентов
А как быть с k? Давайте разберемся. Как узнать по графику, положительный ли коэффициент k или он меньше 0? Посмотрим на графики на рисунке выше: они наклонены в разные стороны. Вот за наклон-то как раз и отвечает коэффициент k, и по наклону прямой мы “вычислим” его знак.
Признак такой: если прямая образует острый угол с положительным направлением оси х, то коэффициент k – положительный. Если прямая образует тупой угол с положительным направлением оси х, то коэффициент k – отрицательный
Посмотрим на наш рисунок:

Коэффициенты уравнения прямой и их значение
У красной и розовой прямых – положительный коэффициент наклона, у зеленой – отрицательный.
Чтобы определить оба коэффициента (а не только их знаки), нужно взять 2 точки на прямой (любые) и подставить их координаты в уравнение прямой. Тогда мы получим систему уравнений, которая позволит определить оба коэффициента. В отдельных случаях можно обойтись и одним уравнением: если прямая проходит через начало координат, или если можно определить коэффициент b по рисунку. Примеры:
Определим коэффициент k для прямой, изображенной на рисунке:

Определение коэффициента наклона прямой
Так как прямая проходит через начало координат, то  . Тогда, чтобы определить k, потребуется всего одно уравнение. Возьмем любую точку, принадлежащую прямой, например, точку (1;3) – точки удобно брать с целыми координатами. Подставляем координаты точки в уравнение прямой вместо x и y:
. Тогда, чтобы определить k, потребуется всего одно уравнение. Возьмем любую точку, принадлежащую прямой, например, точку (1;3) – точки удобно брать с целыми координатами. Подставляем координаты точки в уравнение прямой вместо x и y:

Еще пример:

Определение обоих коэффициентов уравнения прямой
Определим уравнение прямой, для этого найдем коэффициенты b и k ее уравнения. Возьмем две точки на прямой, хорошо, если координаты точек целые. У нас это точки (5;0) и (-3;-2). В общее уравнение прямой подставим координаты этих точек:

Вычтем второе уравнение из первого, это позволит определить коэффициент k:

Чтобы найти b, подставим найденный коэффициент наклона в любое из двух уравнений:

Тогда уравнение этой прямой будет таким:

Иногда коэффициент наклона помогает определить знание следующего факта: если прямая лежит под углом 45 или 135 градусов к оси х (то есть проходит по диагоналям клеточек – как красные прямые на рисунке) – то модуль ее коэффициента наклона равен 1. Если прямая “прижимается” к оси y – желтая область на рисунке – то модуль ее коэффициента наклона больше 1. Если же она “жмется” к оси х (зеленая область) – модуль ее коэффициента k меньше 1. Данный факт помогает при решении таких задач, где необходимо сопоставить графики нескольких прямых и данные уравнения. Тем не менее, чтобы не ошибиться, лучше все же определить коэффициент аналитически: подставив координаты выбранной точки в уравнение.

Коэффициенты прямой, которые превосходят 1 по модулю, и меньше 1 по модулю
Пример такого задания:
Один из графиков на рисунке – график функции y=3x. Каким цветом он изображен?

Определение коэффициента наклона по графику
Рассуждаем так: коэффициент наклона положительный – угол наклона прямой к оси х будет острым – ни зеленый, ни желтый графики не подходят. Модуль коэффициента наклона больше 1 (равен 3) – прямая будет располагаться ближе к оси у, чем к оси х: значит, это график голубого цвета. После этих рассуждений надо обязательно (!) проверить их правильность: просто теперь нам придется проверять не все графики, а только один: голубому графику принадлежит точка (1;3). Подставим ее в уравнение:

Получилось тождество, значит, мы правы. Посмотрите видео-исследование прямой:
Переходим теперь к параболе. Парабола задается квадратичной функцией: . Коэффициент а определяет форму параболы, а также направление ее ветвей: если он положителен – то ветви параболы смотрят вверх, если отрицателен – вниз. От коэффициента b зависит расположение вершины параболы, то есть, в конечном счете, сдвиг по оси х вправо-влево. Наконец, коэффициент с показывает, какова ордината точки, в которой парабола пересечет ось y.
. Коэффициент а определяет форму параболы, а также направление ее ветвей: если он положителен – то ветви параболы смотрят вверх, если отрицателен – вниз. От коэффициента b зависит расположение вершины параболы, то есть, в конечном счете, сдвиг по оси х вправо-влево. Наконец, коэффициент с показывает, какова ордината точки, в которой парабола пересечет ось y.
Рассмотрим несколько графиков, чтобы отработать определение последнего коэффициента – с, как наиболее простого.

Общий вид парабол с разными коэффициентами
Итак, с – точка пересечения параболой оси y. Для первой параболы на рисунке это 8, для второй – 3, для третьей – 6, для четвертой – (-5). А вот точка пересечения пятого графика с осью y только угадывается. Можно сказать с определенностью, что коэффициент с для нее меньше ноля. Однако его точное значение зависит также и от формы параболы, которая определяется величиной коэффициента a. Если этот коэффициент задан и равен (-1), то можно догадаться, что с для нее равен (-19). Однако. чтобы точно определить все коэффициенты, необходимо взять несколько точек, принадлежащих этому графику функции, и, подставив их координаты в уравнение квадратичной функции, решить систему уравнений, которая и позволит точно найти a,b и с.
Разберем такое задание: график какой из приведенных ниже функций изображен на рисунке?

Подбор формулы, задающей график функции

Посмотрим на график. Ветви параболы направлены вверх, значит, коэффициент a – положительный. Тогда нам не подойдут ни первая, ни последняя функция. Две оставшиеся отличаются одним лишь знаком коэффициента b, поэтому найдем абсциссу вершины параболы. Для второй:

Для третьей:

Тогда, значит, подходит вторая функция, так как видно, что вершина лежит в области отрицательных значений х.
Следующая задача такая: найдите значение а по графику функции  , изображенному на рисунке.
, изображенному на рисунке.

Парабола, у которой коэффициент а=1
Есть два пути для решения данной задачи. Первый – рациональный. Находим точки, принадлежащие графику, подставляем их координаты в уравнение, получаем систему (как минимум, понадобится три точки, чтобы определить три коэффициента, и система будет из трех уравнений), решаем систему.
Есть и второй путь – эмпирический. Этот метод “тыка” иногда упрощает задачу очень существенно, тем более что “тык” будет у нас вполне обоснованным, а не случайным.
Давайте рассуждать:ветви направлены вверх? – коэффициент а – положительный. Где находится вершина параболы? Правильно, в точке (2;0). Значит, ее ось симметрии –

Парабола, у которой коэффициент а=1
прямая х=2. Тогда все ее точки должны располагаться симметрично по обе стороны от этой прямой.
Возьмем две точки на оси х, отстоящие на единицу от оси симметрии параболы – точки х=1, х=3. Какие им соответствуют ординаты? y=1 в обоих случаях. Теперь возьмем точки, отстоящие на 2 единицы от оси симметрии – х=0 и х=4. Какие ординаты будут им соответствовать? y=4! Иными словами, ординаты точек этого графика получаются, если просто возводить в квадрат разность абсцисс точки и вершины параболы:  и т.д. Тогда коэффициент a этой параболы равен 1!
и т.д. Тогда коэффициент a этой параболы равен 1!
Наши рассуждения можно пояснить рисунком:
Теперь рассмотрим задачи более сложные, связанные как раз с необходимостью составлять систему уравнений.
Иногда вершина предлагаемого графика располагается не в пересечении клеточек, то есть координаты вершины – дробные числа. Кроме того, форма параболы отличается от “классической”, которую мы получаем, если а=1. Тогда “метод научного тыка” не годится, “на глазок” коэффициенты уже не определить. Вот здесь необходимо найти принадлежащие графику точки, лучше, если они будут находиться на пересечении клеток, то есть их координаты будут целыми. Сколько же потребуется таких точек? Если возможно определить коэффициент с по графику, то две, а если нельзя – три.
Рассмотрим задачу: необходимо найти все коэффициенты уравнения, задающего график:

Найти все коэффициенты по графику функции
Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:
координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:

Последние два уравнения вычтем:

Данное выражение подставим в первое и второе уравнения:

Вычтем два получившихся уравнения:
 Зная а, можем найти и остальные коэффициенты:
Зная а, можем найти и остальные коэффициенты:

Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:

Найти все коэффициенты по графику функции
Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):

Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:


Найти все коэффициенты по графику функции
Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:
Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.
Точки будут: (-2; -3),(-5; -3) и (-3; -5) . Тогда уравнения:

Из первого уравнения вычитаем второе:

Полученное подставим в первое и третье:

Полученные уравнения вычтем вновь, и найдем искомое:

Посмотрите видео-исследование параболы:
Наконец, нужно познакомиться с гиперболой. График ее задается функцией:  . Он интересен тем, что располагается всегда в двух квадрантах: в первом и третьем, либо во втором и четвертом. От знака коэффициента k зависит вид функции: если знак положителен, то ветви гиперболы расположатся в первом и третьем квадрантах, если отрицателен – во втором и четвертом. Кроме того, от этого коэффициента зависит и форма гиперболы. Если
. Он интересен тем, что располагается всегда в двух квадрантах: в первом и третьем, либо во втором и четвертом. От знака коэффициента k зависит вид функции: если знак положителен, то ветви гиперболы расположатся в первом и третьем квадрантах, если отрицателен – во втором и четвертом. Кроме того, от этого коэффициента зависит и форма гиперболы. Если  , то гипербола непременно пройдет через точки (1;1), (-1;-1). Если
, то гипербола непременно пройдет через точки (1;1), (-1;-1). Если  , то гипербола будет “прижиматься” к осям координат, а если , то наоборот, точки графика будут лежать дальше от начала координат. Это иллюстрирует рисунок (одна клеточка – единичный отрезок):
, то гипербола будет “прижиматься” к осям координат, а если , то наоборот, точки графика будут лежать дальше от начала координат. Это иллюстрирует рисунок (одна клеточка – единичный отрезок):

Коэффициент гиперболы
Здесь зеленая область – область, где лежат точки гипербол с положительным коэффициентом k, меньшим 1. Желтая область – область точек гипербол с положительным коэффициентом k, большим 1. Черным цветом изображена “классическая” гипербола, k=1.
Для отрицательных k (одна клеточка – единичный отрезок):

Коэффициент гиперболы
Разберем задачу: нужно определить, график какой из приведенных ниже функций изображен на рисунке.

Коэффициент гиперболы

Рассмотрим график. Все его точки лежат во второй и четвертой четвертях, это означает, что положительным х соответствуют отрицательные y, а отрицательным – положительные, то есть коэффициент у функции, задающей этот график, должен быть отрицательным. Тогда ни первая, ни третья функции не подходят. Значит, надо выбирать из второй и четвертой, причем у второй  , а у четвертой
, а у четвертой  . Значит, график второй функции должен быть расположен ближе к осям координат, чем точка (1;-1) – голубая область на предыдущем рисунке. У нас график расположен не так, если бы мы перенесли его на предыдущий рисунок, он бы попал в серую область, значит, предположительно, изображен график четвертой функции, однако, в этом надо быть уверенным наверняка. Поэтому возьмем точку на графике и подставим ее координаты в уравнение, например, точку (3;-1):
. Значит, график второй функции должен быть расположен ближе к осям координат, чем точка (1;-1) – голубая область на предыдущем рисунке. У нас график расположен не так, если бы мы перенесли его на предыдущий рисунок, он бы попал в серую область, значит, предположительно, изображен график четвертой функции, однако, в этом надо быть уверенным наверняка. Поэтому возьмем точку на графике и подставим ее координаты в уравнение, например, точку (3;-1):

Получилось тождество, значит, уравнение выбрано верно.
Еще задача:
На одном из графиков изображен график функции  . Какой это рисунок?
. Какой это рисунок?

Определение графика по заданной функции
Во-первых, не все изображенные графики – гиперболы. Сразу отбросим “лишние” – это розовый график функции  – номер 2, и фиолетовый – номер 1, который расположен “не в тех” квадрантах. Остаются два графика – 3 и 4 – которые очень похожи друг на друга. Поскольку коэффициент перед х в заданной функции отрицательный, нам нужен 4 график – тот, что изображен черным цветом.
– номер 2, и фиолетовый – номер 1, который расположен “не в тех” квадрантах. Остаются два графика – 3 и 4 – которые очень похожи друг на друга. Поскольку коэффициент перед х в заданной функции отрицательный, нам нужен 4 график – тот, что изображен черным цветом.
Последняя задача: найдите коэффициент k по графику функции  , изображенному на рисунке:
, изображенному на рисунке:

Определение коэффициента функции по графику
Здесь достаточно взять только одну точку, принадлежащую графику, и подставить ее координаты в уравнение:

Посмотрите короткое видео с исследованием гиперболы:
Надеюсь, эта статья поможет вам в подготовке к экзамену! Всего вам хорошего, вопросы можно задать в комментариях, я постараюсь ответить.
Алгоритм нахождения коэффициентов a, b, c квадратичной функции по графику
Инфоурок › Математика ›Другие методич. материалы›Алгоритм нахождения коэффициентов a, b, c квадратичной функции по графику
Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: 389899
Похожие материалы
Оставьте свой комментарий
Как легко составить уравнение параболы по графику
Автор Сергей Валерьевич
Среда, 3 августа, 2016
В данной статье репетитор по математике рассказывает о простом и эффективном способе составления уравнения параболы по её графику, которому вас не научат в школе. Дочитайте эту статью до конца или посмотрите видео с подробным объяснением, потому что эта информация может вам пригодиться на экзамене.
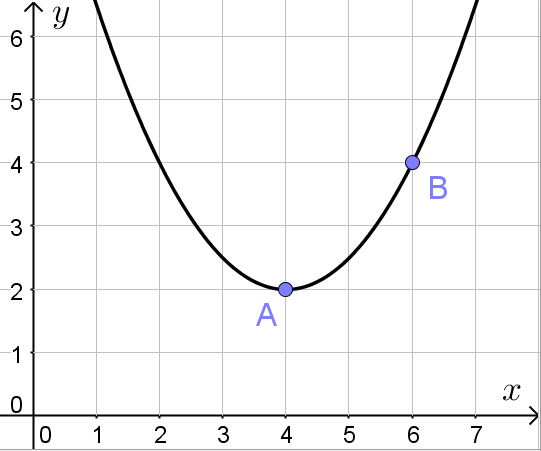
Задача состоит в том, чтобы по графику параболы (см. рисунок) определить коэффициенты a, b и c соответствующей квадратичной функции 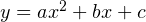 :
:
Существует стандартный и крайне неэффективный способ решения этой задачи. Он заключается в том, чтобы через координату 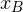 вершины параболы связать коэффициенты a и b, используя формулу
вершины параболы связать коэффициенты a и b, используя формулу 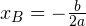 . Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
. Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
Мы не пойдём этим путём. Предлагаемый в данной статье способ намного более прост и изящен. Введём новую систему координат  с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид:
с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид: 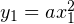 , где
, где 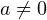 . Изобразим в новой системе координат график квадратичной функции
. Изобразим в новой системе координат график квадратичной функции 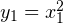 (синяя пунктирная линия на рисунке):
(синяя пунктирная линия на рисунке):
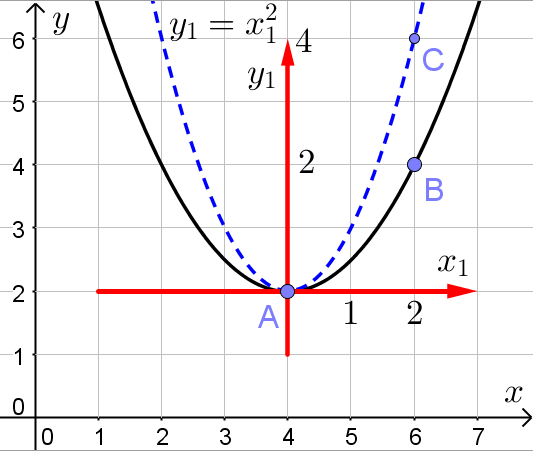
Абсциссы точек C и B в новой системе координат равны. Ордината точки C в 2 раза больше ординаты точки B. Значит график исходной параболы в новой системе координат получен умножением на 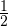 всех ординат точек графика функции
всех ординат точек графика функции 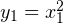 . Откуда получаем, что
. Откуда получаем, что 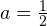 . Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат:
. Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат: 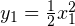 .
.
Осталось перейти в исходную систему координат. Поскольку новая система координат получена путём параллельного переноса исходной системы координат на 4 единичных отрезка вправо и 2 единичных отрезка вверх, то в исходной системе координат наша парабола может быть представлена в виде следующего выражения:
![Rendered by QuickLaTeX.com \[ y = \frac{1}{2}(x-4)^2+2 = \frac{1}{2}x^2-4x+10. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e7cec75d95818cca2330023c1ec246b7_l3.png)
Как видите, данный способ требует минимум вычислений и фактически является полуустным. Запомните этот способ, он может пригодиться вам при решений задач из ЕГЭ, ОГЭ или вступительных экзаменов в вузы и школы с углубленным изучением математики.
Статья написана репетитором по математике в Москве, Сергеем Валерьевичем
Линейная функция
Функция называется линейной, если ее можно записать в виде \(y=kx+b\), где \(k\) и \(b\) -некоторые числа.
Примеры:
|
\(y=\frac{1}{3}x-5\) |
\(k=\frac{1}{3}\), \(b=-5\) |
|
|
\(y=2x\) |
\(k=2\), \(b=0\) |
|
|
\(y=8\) |
\(k=0\), \(b=8\) |
Функция не всегда сразу задана в виде \(y=kx+b\), иногда такой вид получится только после преобразований. Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
График линейной функции всегда представляет собой прямую линию – отсюда и название: «линейная функция».
Чтобы в этом убедиться построим графики функций \(y=2x\), \(y=\frac{1}{3}x-5\), \(y=8\).
Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
Как меняется график при разных \(k\)?
Чтобы определить, как влияет на график коэффициент \(k\), построим несколько функций разными \(k\): \(\frac{1}{3}\),\(-\frac{1}{3}\),\(2\),\(-2\) и \(0\). При этом во всех функциях сделаем \(b\) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: \(y=\frac{1}{3}x\), \(y=-\frac{1}{3}x\), \(y=2x\), \(y=-2x\), \(y=0\).
Заметьте, что при \(k=2\) и \(\frac{1}{3}\) — функция возрастает, а при \(k=-2\) и \(-\frac{1}{3}\) — убывает. На самом деле:
При любом \(k>0\) функция возрастает и при любом \(k<0\) — убывает. Когда же \(k=0\) — она не возрастает и не убывает, а идет параллельна оси \(x\) (или совпадает с ней).
Так же можно заметить, чем больше модуль \(k\), тем «круче» график.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).
Как меняется график при разных значениях \(b\)?
Чтобы определить, как \(b\) влияет на график, построим несколько функций с разными \(b\): \(6\), \(2\), \(0\), \(-3\) и \(-8\). При этом \(k\) пусть во всех функциях будет равен \(2\).
Не сложно заметить, что прямая либо поднимается на \(b\) (если \(b>0\)) либо опускается на \(|b|\) если
(\(b<0\)).
Как по графику функции определить значение \(b\)?
Очень просто — прямая пересекает ось \(y\) всегда в точке \(b\). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида \(y=kx+b\). Установите соответствие между графиками функций и знаками коэффициентов \(k\) и \(b\).
A. B.C.
Коэффициенты
| 1) \(k>0\),\(b>0\) | 2) \(k<0\), \(b>0\) | 3) \(k<0\), \(b<0\) | 4) \(k>0\), \(b<0\) |
Решение:
А. – функция убывает, поэтому \(k<0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 2).
B. — функция возрастает — \(k>0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 1).
C. – функция убывает — \(k<0\). Точка пересечения оси \(y\) и прямой находится ниже нуля, значит \(b<0\). Подходит вариант под цифрой 3).
Ответ: 213.
«Читерский» способ строить график линейной функции
Можно конечно строить график линейной функции по точкам, как описано здесь, но можно и быстрее, буквально в три шага:-
Отмечаем точку \(b\) на оси игреков.
-
От неё идем вправо на количество клеточек равное знаменателю \(k\), и вверх на количество клеточек равное числителю \(k\) (если \(k>0\)) или вниз на тоже количество (если \(k<0\)).
-
Проводим через эти две точки прямую.
Пример: Построить график функции \(y=3x+1\).
|
Шаг 1. \(b=1\), поэтому отмечаем точку с этим значением на оси \(y\)
|
Шаг 2. \(k=3\), а тройка это тоже самое, что \(\frac{3}{1}\). При этом \(k>0\). Поэтому идем вправо на единицу и вверх на \(3\). Ставим точку. |
Шаг 3. Проводим через эти две точки прямую. |
Пример: Построить график функции \(y=-\frac{1}{4} x-3\).
|
Шаг 1. \(b=-3\) отмечаем точку с этим значением на оси \(y\).
|
Шаг 2. \(k=-\frac{1}{4}\), \(k<0\), числитель \(1\), знаменатель \(4\). Значит, идем вправо на \(4\) и вниз на единицу. |
Шаг 3. Проводим через эти две точки прямую. |
Немного потренируйтесь и вы сами поймете, какой это классный способ строить линейную функцию.
Скачать статьюЗнаки коэффициентов квадратного трехчлена
Знаки коэффициентов квадратного трехчлена.
В этой статье я расскажу, как по графику квадратичной функции найти знаки коэффициентов квадратного трехчлена.
Чтобы определить знаки коэффициентов квадратного трехчлена по графику квадратичной функции  , нужно вспомнить теорему Виета.
, нужно вспомнить теорему Виета.
Согласно теореме Виета, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.
Квадратное уравнение называется приведенным, если его старший коэффициент равен единице.
Чтобы уравнение  стало приведенным, нужно обе части уравнения разделить на старший коэффициент. Получим приведенное уравнение
стало приведенным, нужно обе части уравнения разделить на старший коэффициент. Получим приведенное уравнение  . Для него справедливы соотношения:
. Для него справедливы соотношения:

И эти же соотношения справедливы для уравнения 
По графику квадратичной функции мы легко можем определить знак коэффициента  — если ветви параболы направлены вверх, то
— если ветви параболы направлены вверх, то 
 , а если вниз, то
, а если вниз, то 
 .
.
Также по графику легко определяются знаки корней (корни квадратного трехчлена  — это абсциссы точек пересечения графика функции
— это абсциссы точек пересечения графика функции  с осью абсцисс), а также знак корня с большим модулем.
с осью абсцисс), а также знак корня с большим модулем.
Если оба корня положительны, то 
 .
.
Если оба корня отрицательны, то 
 .
.
Если корень с большим модулем положителен, то 
 .
.
Если корень с большим модулем отрицателен, то 
 .
.
Если корни имеют одинаковые знаки, то 
 .
.
Если корни имеют разные знаки, то 
 .
.
Во всех случаях, определив знак коэффициента  по направлению ветвей параболы, мы легко найдем знаки коэффициентов
по направлению ветвей параболы, мы легко найдем знаки коэффициентов  и
и 
Рассмотрим примеры.
1. Определить знаки коэффициентов квадратного трехчлена  , если график функции
, если график функции  имеет вид:
имеет вид:

1. Ветви параболы направлены вниз, следовательно, 
 .
.
2. Корни имеют одинаковые знаки, следовательно, их произведение положительно: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
3. Оба корня отрицательны, следовательно, их сумма отрицательна: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
Ответ: 
 ,
, 
 ,
, 
 .
.
2. Определить знаки коэффициентов квадратного трехчлена  , если график функции
, если график функции  имеет вид:
имеет вид:

1. Ветви параболы направлены вверх, следовательно, 
 .
.
2. Корни имеют разные знаки, следовательно, их произведение отрицательно: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
3. Корень с большим модулем положителен, следовательно, сумма корней положительна: 
 . Так как
. Так как 
 , следовательно,
, следовательно, 
 .
.
Ответ: 
 ,
, 
 ,
, 
 .
.
Замечание:  — ордината точки пересечения параболы с осью
— ордината точки пересечения параболы с осью  , поэтому знак
, поэтому знак  можно определить сразу.
можно определить сразу.

Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида  , где
, где 
 называется квадратичной функцией.
называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:
имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции  , составим таблицу:
, составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент  , то график квадратичной функции имеет ровно такую же форму, как график функции
, то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.
при любых значениях остальных коэффициентов.
График функции  имеет вид:
имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции  симметричен графику функции
симметричен графику функции  относительно оси ОХ.
относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции
— это точки пересечения графика функции  с осью ОХ.
с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции  с осью ОХ, нужно решить уравнение
с осью ОХ, нужно решить уравнение  .
.
В случае квадратичной функции  нужно решить квадратное уравнение
нужно решить квадратное уравнение  .
.
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант:  , который определяет число корней квадратного уравнения.
, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если 
 ,то уравнение
,то уравнение  не имеет решений, и, следовательно, квадратичная парабола
не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если
не имеет точек пересечения с осью ОХ. Если 
 ,то график функции выглядит как-то так:
,то график функции выглядит как-то так:

2. Если 
 ,то уравнение
,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола
имеет одно решение, и, следовательно, квадратичная парабола  имеет одну точку пересечения с осью ОХ. Если
имеет одну точку пересечения с осью ОХ. Если 
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:

3. Если 
 ,то уравнение
,то уравнение  имеет два решения, и, следовательно, квадратичная парабола
имеет два решения, и, следовательно, квадратичная парабола  имеет две точки пересечения с осью ОХ:
имеет две точки пересечения с осью ОХ:
 ,
, 
Если 
 ,то график функции выглядит примерно так:
,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:



Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы  с осью OY.
с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль:
с осью OY, нужно в уравнение параболы вместо х подставить ноль:  .
.
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой  .
.
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 
1. Направление ветвей параболы.
Так как 
 ,ветви параболы направлены вверх.
,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 



Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение: 
 ,
, 
3. Координаты вершины параболы:


4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы


Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид  — в этом уравнении
— в этом уравнении  — координаты вершины параболы
— координаты вершины параболы
или в уравнении квадратичной функции 
 , и второй коэффициент — четное число.
, и второй коэффициент — четное число.
Построим для примера график функции  .
.
Вспомним линейные преобразования графиков функций. Чтобы построить график функции  , нужно
, нужно
- сначала построить график функции
 ,
, - затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции  . В уравнении этой функции
. В уравнении этой функции  , и второй коэффициент — четное число.
, и второй коэффициент — четное число.
Выделим в уравнении функции полный квадрат: 
Следовательно, координаты вершины параболы:  . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
. Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда 
2. Координаты вершины параболы: 

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.
Перед вами график квадратичной функции вида  .
.
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции  от значения коэффициента
от значения коэффициента  ,
,
— сдвига графика функции  вдоль оси
вдоль оси  от значения
от значения  ,
,
— сдвига графика функции  вдоль оси
вдоль оси  от значения
от значения 
— направления ветвей параболы от знака коэффициента 
— координат вершины параболы  от значений
от значений  и
и  :
:
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
По расписанию — определение по расписанию The Free Dictionary
sched · ule
(skĕj′o͞ol, -o͞o-əl, skĕj′əl) n.1. Список времени отправления и прибытия; расписание: расписание автобусов; расписание экскурсий.
2. План выполнения работы или достижения цели с указанием порядка и отведенного времени для каждой части: завершение проекта в срок.
3. Печатный или письменный список предметов в табличной форме: расписание почтовых тарифов.
4.а. Программа мероприятий или встреч, ожидаемых в определенное время: Можете ли вы вписать меня в свое расписание во вторник днем?
б. Студенческая программа занятий.
5. Дополнительная информация, приложенная к документу.
6.а. Перечень контролируемых веществ, регулируемый на федеральном уровне, с разбивкой по классам по возможности злоупотребления.
б. Один из рангов или классов в таком списке.
тр.в. график , график , график1. Чтобы ввести график: рассчитайте и запланируйте каждый налоговый вычет в соответствующей форме.
2. Чтобы составить расписание для: Я еще не запланировал следующую неделю.
3. Чтобы спланировать или назначить на определенное время или дату: запланированная поездка на июнь; должен был прибыть в понедельник.
4. Для включения или ранжирования (контролируемое вещество) в списке.
[среднеанглийский sedule, лист пергамента или бумаги, примечание , от старофранцузского cedule, от позднего латинского schedula, уменьшительное от scheda, вариант латинского scida, полоска папируса , от греческого skhida, skhedē; возможно сродни схизеину, к расколу ; см. шизо- .]
щед’лар прил.
щедь · лер н.
график
(ˈʃɛdjuːl; esp US skɛdʒʊəl) n1. план действий по проекту, распределение работ и время для этого
2. список позиций: график фиксированных цен.
3. список времени, особенно прилетов и отъездов; расписание
4. список задач, которые должны быть выполнены, особенно в течение установленного периода
5. (закон) закон список или инвентарь, обычно дополняющий контракт, будет и т. д.
6 по расписанию в ожидаемое или запланированное время
vb ( tr )7., чтобы составить расписание или поместить в расписание
8. , чтобы запланировать появление в определенное время
[C14: ранее cedule, sedule через старофранцузский от поздней латыни schedula небольшой лист бумаги, из латинского scheda лист бумаги]
ˈschedular adj
sched • ule
(ˈskɛdʒ ul, -ʊl, -u əl; Brit. ˈʃɛd yul, ˈʃɛdʒ ul4,)
v. -uled, -ul • ing. н.
1. план действий, ус. написано для предлагаемой цели, особенно со ссылкой на последовательность событий и время, отведенное для каждого: Они завершили проект в срок.
2. ряд вещей, которые нужно сделать, или событий, которые должны произойти в или в течение определенного времени или периода: У него всегда есть полное расписание.
3. расписание.
4. письменное или печатное заявление с подробностями, часто в табличной форме, особенно.в качестве дополнения к другому документу.
5. Обс. письменная работа.
в.т.6. , чтобы составить расписание или войти в расписание.
7. запланировать на определенную дату: запланировать публикацию на июнь.
[1350–1400; Среднеанглийский cedule, sedule schedula = sched (a) papyrus strip (alter. Лат. Scida) + Latin -ula -ule]sched′ul • er, n.
расписание
— восходит к греческому skhede, что означает «лист папируса»; оно начиналось с билета или краткой заметки. См. также термины, относящиеся к папирусу.График
Past причастие: запланировано
Герундий: планирование
ImperativePresentPreteritePresent ContinuousPresent PerfectPast ContinuousPast PerfectFutureFuture PerfectFuture ContinuousPresent Идеальный ContinuousFuture Идеальный ContinuousPast Идеальный ContinuousConditionalPast Условный
| императив |
|---|
| График |
| График |
| Настоящее | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Я планирую | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| вы планируете | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| он / она / она расписывает | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| мы планируем | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| вы планируете | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
26 они
Управление расписанием проекта Согласно PMBOKПоскольку проект определяется как временное мероприятие (PMBOK 1.1), крайние сроки включены в критерии успеха всех проектов. Поскольку у всех проектов есть определенная конечная точка, обстоятельства вокруг этой конечной точки могут привести к успеху или неудаче проекта. Управление графиком проекта может быть одной из самых сложных частей управления проектом. Я видел больше разрушенных отношений с клиентами в этой области управления проектами, чем в любой другой.Тайм-менеджмент необходим для достижения успешных проектов. Вот почему График
План управления расписаниемЭто включает в себя создание Плана управления расписанием, а также разработку ожиданий относительно того, как график будет соблюдаться. Входы
Инструменты и методы
Выходы
Определить действияНа этом этапе определяются и детализируются действия, необходимые для завершения проекта.Он отличается от графика декомпозиции работ (WBS) в области знаний по управлению содержанием проекта тем, что действия являются более точными. То есть СПП-элемент будет содержать несколько действий. При этом у меня были небольшие проекты, где я просто называл WBS и действия одним и тем же. PMBOK позволяет это делать в небольших проектах. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Present | ||
| Я, вы, мы, они | график | |
| он, она, это | графики | |
| > Посмотреть больше | ||
| Прошлое | ||
| Я, ты, он, она, оно, мы, они | запланировано | |
| Настоящее совершенное | ||
| Я, ты, мы, они | запланировали | |
| он, она, это | запланировал | |
| Прошлое совершенное | ||
| Я, ты, он, она, это, мы, они | запланировал | |
| Будущее | ||
| Я, ты, он, она , это, мы, они | будут планировать | |
| Future perfect | ||
| Я, ты, он, она, это, мы, они | будут планировать | |
| > Посмотреть меньше | ||
| Настоящее время | ||
| I | Я планирую | |
| он, она, это | составляет расписание | |
| > Посмотреть больше | ||
| вы, мы, они | планируем | |
| Прошлое | ||
| Я, он, она, это | планировал | |
| вы, мы, они | планировали | |
| Я, ты, мы, они | составляли расписание | |
| он, она, это | составляло расписание | |
| Прошлое совершенное | ||
| Я, ты, он, она, оно, мы, они | планировали | |
| Future | ||
| Я, ты, он, она, это, мы, они | будем планировать | |
| Future perfect | ||
| Я, ты, он , она, она, мы, они | будут планировать | |
| > Посмотреть меньше | ||
Найдите свой хронотип и запланируйте производительность
Есть много советов о связи между временем и продуктивностью: статьи, в том числе и наша собственная, в которых предлагаются «Х вещей, которые нужно сделать утром / днем / вечером», чтобы оставаться продуктивным в течение всего дня.
И да, , когда вы работаете над определенными типами задач, абсолютно влияет на вашу производительность. Но выбор времени не является универсальным подходом. Зачем? Потому что у каждого из нас есть уникальный хронотип: внутренние часы, которые управляют нашим вниманием, творчеством и настроением в течение дня.
Чтобы понять, когда вам следует работать над каждым делом, которого вы хотите достичь, вам нужно определить свой хронотип. Как только вы поймете свой хронотип — и начнете использовать это понимание для планирования своих ежедневных задач, — ваша продуктивность возрастет до необходимого уровня.
Что такое хронотип?
Хронотип — это научный термин, обозначающий то, что мы обычно называем внутренними часами. И хотя мы обычно говорим о наших внутренних часах с точки зрения нашей естественной склонности засыпать и просыпаться в определенные часы дня, хронотипы определяют гораздо больше, чем просто цикл сна.
Ваш личный хронотип влияет на то, в какое время суток вы наиболее сосредоточены, наиболее креативны, с наибольшей вероятностью совершите ошибку, с большей вероятностью пребываете в хорошем или плохом настроении и многое другое.
Если вы работаете в офисе, вы, вероятно, заметите, что большинство людей начинают уставать и отвлекаться в период с раннего до середины дня — как часы. Вы можете списать это на спад после обеда, но какой бы ни была причина, большинство из нас не может позволить себе терять три часа в день из-за низкого уровня энергии и блуждающих умов.
Чтобы лучше понять концепцию хронотипа и его влияние на повседневную (или, скорее, часовую) продуктивность, мы обратимся к книге Дэниела Х. Пинка Когда: научные секреты идеального времени . В нем он рассматривает научные исследования, которые доказывают, что фраза «время — это все» — не просто клише. По словам Пинка (и сотен научных исследований, на которые он опирался при написании книги), каждый — люди любого возраста, пола и расы, во всех географических точках и часовых поясах — каждый день испытывает три фазы продуктивности. :
Для большинства людей это выглядит так:
Как раз между обедом и концом рабочего дня — самая низкая точка дня, если не считать моментов после пробуждения.
Итак, если вы начинаете чувствовать себя менее энергичным и сосредоточенным каждый день после обеда, это естественно. Но что это значит для вашей производительности? Означает ли это, что вы должны отказаться от работы в течение этих трех часов и смириться с выполнением всех задач утром?
Не обязательно.
Время для каждой цели
В часы, предшествующие и на пике, мы наиболее сосредоточены, меньше всего отвлекаемся и думаем наиболее ясно.Это идеальное время для аналитических задач.
Но это не значит, что желоб — это полная потеря. На самом деле лучше для творческих задач. По словам Пинк, творчество процветает, когда нас легче отвлечь, потому что отвлекающие факторы на самом деле помогают нам устанавливать связи, которых мы, возможно, не установили бы, если бы были очень сосредоточены.
Это означает, что можно оставаться продуктивным в течение всего дня — даже во время кормушки — если просто запланировать время для выполнения нужных задач в нужное время дня:
- До и во время пика поработайте над аналитическими задачами .
- В период с по работайте над творческими задачами .
Вот пример из моей собственной работы. Моя работа состоит из четырех основных задач:
Ideating: Придумывать идеи для написания — это самая творческая задача, за которую я отвечаю. Упражнение начинается с «Эм…» и заканчивается питчем для статьи, которую я хочу написать и не стесняюсь отправить своим редакторам.
Исследование: Все, что я пишу, требует определенного исследования.Иногда это просто SEO-исследование. Иногда нужно читать книгу или играть с десятками приложений, чтобы найти лучшее. Исследования требуют много внимания, поэтому я считаю это более аналитической задачей.
Наброски: Иногда я просто начинаю писать, но чаще я начинаю с наброска. Создание схемы — задача творческая. Я должен точно определить, о чем я хочу написать, и в каком порядке имеет смысл излагать информацию.
Writing: Хотя мы склонны думать о письме как о творческой задаче — и, возможно, так было бы, если бы я писал стихи или роман, — я пишу гораздо более аналитически.Обычно у меня уже есть набросок, поэтому написание — это простой способ сосредоточиться и получить слова на странице.
Теперь, когда я понял свой хронотип и определил, за какие задачи я отвечаю, я могу использовать эту информацию для создания ежедневного расписания, которое повысит мою продуктивность. Мне нужно работать над своими аналитическими задачами (исследовать и писать) по утрам, когда я нахожусь на пике карьеры. Затем, во время дневного кормления, я должен сосредоточиться на своих творческих задачах (набросок и размышления).
Если вы начнете планировать свою работу в соответствии со своим хронотипом, вы станете более продуктивным — и, вероятно, более счастливым из-за этого.
Типы хронотипа
Первым шагом в создании индивидуального графика продуктивности является определение вашего хронотипа. Этот шаг имеет решающее значение, потому что, хотя большинство людей следуют ритму, который я описал до сих пор — пик утром, минимум днем, отскок вечером, — не все делают.
По словам Пинка, существует три различных типа хронотипа: жаворонок, третья птица и сова:
Жаворонки — это то, что мы считаем утренними людьми.По собственному желанию — и даже не по работе — они встают с постели до 7 часов утра
Третьи птицы — наиболее распространенный хронотип. Третьи птицы по своей природе склонны просыпаться между 8 и 10 часами утра
Совы — ночные люди. В дни, когда им не нужно вставать для работы или выполнения каких-либо других обязательств, они не встают с постели до 10 часов утра
.
Вот почему важно понимать свой хронотип: в то время как жаворонки и третьи птицы переживают день на пике, впадине и восстановлении, полуночники переживают день в обратном порядке: восстановление, впадина и пик.Так что, если вы сова, вы наиболее сосредоточены и, следовательно, способны выполнять аналитические задачи вечером.
Найдите свой хронотип
Pink предлагает несколько советов по поиску вашего хронотипа.
Предложение 1
Самый простой способ — ответить на три вопроса. Когда работа или другие обязанности не заставляют вас ложиться спать или просыпаться в определенное время — когда ваше расписание полностью зависит от вас:
- Во сколько вы обычно ложитесь спать?
- В какое время вы обычно просыпаетесь?
- Какая середина между этими двумя временами?
Например, если вы обычно ложитесь спать в 2 часа ночи.м. и просыпаешься в 10 утра, твоя середина 6 утра
Затем найдите на этой диаграмме свое среднее время, чтобы определить свой хронотип:
Если вы чувствуете себя уверенно с этим методом, отлично. Я был немного скептически настроен, потому что, когда я ложусь спать и встаю по выходным, это действительно непоследовательно. Иногда я ложусь спать в 23 часа. и просыпаюсь в 7 утра. Иногда я встаю до 5 утра и не вытаскиваю себя из постели до полудня.
Если вы не уверены в своих результатах, есть несколько других способов найти свой хронотип.
Предложение 2
Один из вариантов — пройти автоматизированный опросник по утрам и вечерам (Auto-MEQ).
Затем используйте эту шкалу, чтобы преобразовать ваши оценки Auto-MEQ в жаворонок, третью птицу и сову:
- Если вы наберете 70-86 очков, вы жаворонок.
- Если вы наберете 31–69 очков, вы на третьем месте.
- Если вы набрали от 16 до 30, вы сова.
Предложение 3
Но если вы хотите быть абсолютно уверены — и вы хотите точно определить, в какое время вы наиболее сосредоточены каждый день — потратьте неделю на заполнение этого Daily When Tracker, созданного Pink.Установите будильник, который будет срабатывать каждые 90 минут, пока вы не спите, а затем заполните соответствующую строку.
В конце недели вы должны увидеть тенденции в том, когда вы чувствуете себя наиболее и наименее бдительным. Используйте это, чтобы определить, как ваши внутренние часы убывают и отклоняются в течение дня.
Связано: Если вы знакомы с The Power of When Майкла Бреуса, вы можете подумать о хронотипах в категориях Бреуса: дельфин, лев, медведь и волк. Чтобы связать эти две терминологии, львы = жаворонки, медведи = третьи птицы и волки = совы.У дельфинов действительно нет эквивалента в подходе Пинка, поэтому, если вы думаете о себе как о дельфине Бреуса, используйте описанные выше методы, чтобы определить, какой из хронотипов Пинка применим к вам.
Создайте свой личный график продуктивности
Теперь, когда вы знаете свой хронотип, пришло время выяснить, когда вам следует работать над различными задачами.
Если вы жаворонок или сторонник, вам больше всего повезет с аналитическими задачами, требующими большого внимания в первые шесть часов вашего дня.Примерно через шесть часов в день вы достигнете пика, а затем на несколько часов он упадет в корыто. Используйте это время для работы над задачами, требующими творчества.
Если вы сова, вы все еще можете выполнить некоторую аналитическую работу утром, так как ваша тенденция растет; вы просто не будете так сосредоточены, как ваши коллеги-жаворонки и третьи птицы. Однако, как и все остальные, у вас будет середина дня, поэтому сосредоточьтесь на творческих задачах. А если вы действительно хотите лучше всего провести аналитическую работу, сделайте это вечером после ужина.
В начале дня или недели посмотрите на все задачи, которые вам нужно выполнить, и разделите их на аналитические и творческие группы. Затем составьте график работы над каждой задачей на основе вашего хронотипа. Вот пример из моей работы:
Если у вас такой же краткий список дел, как у меня, тогда вы можете планировать свою работу ручкой и бумагой, электронной таблицей или просто своим умом. Но если у вас много задач, которые нужно отслеживать и составлять по расписанию, вы можете подумать о принятии такого приложения, как Plan.
Планпоказывает ваш список дел рядом с календарем Google, позволяя вам перетаскивать задачи, чтобы запланировать время для выполнения этих задач в вашем календаре. Это отличный способ организовать задачи в подходящее время дня для вашего хронотипа и не дать людям планировать встречи на ваши наиболее продуктивные часы дня.
Стоимость: Бесплатно для двух пользователей с индивидуальным планом.
Кроме того, вы можете использовать Zap для автоматического создания событий календаря из предпочитаемого вами приложения с делами.
- Если вы используете Календарь Google, попробуйте эти Zap:
- Если вы используете Outlook, попробуйте эти Zap:
Или создайте собственный рабочий процесс, используя любое из тысяч приложений.
Что делать, если ваше расписание не гибкое?
В идеале, вы всегда сможете планировать свои задачи в соответствии с вашим хронотипом. Но что произойдет, если вы не сможете? Что, если вы — сова, вынужденная работать в первую смену, или если у вас нет другого выбора, кроме как работать над аналитической задачей весь день, чтобы уложиться в срок?
Вам не нужно мириться с неоптимальной производительностью.Есть способ повысить вашу продуктивность и сосредоточенность даже во время кормления: сделайте перерыв. Когда мы делаем перерывы в работе, это автоматически освежается. Это не так хорошо, как полноценный ночной сон, но он может вывести вас из спада и помочь вам на короткое время переориентироваться.
Есть много способов сделать перерывы лучше. Оставь свой рабочий стол на обед. Выйдите на улицу и подышите свежим воздухом в течение пяти минут каждый час. Сделайте несколько прыжков или отжиманий. Поговори с другом.
Но вот что действительно важно: перерывы не могут быть просто продолжением работы.
Если вы идете обедать с коллегой и все время разговариваете по магазинам, вы на самом деле не делаете перерыв, потому что не даете своему разуму времени расслабиться. Если вы проверяете электронную почту на своем телефоне, сидя на улице на солнышке, вы не делаете перерыва. Что касается вашего разума, вы все еще работаете.
Если вы не можете распределить творческую работу в часы, когда вы усердно трудитесь, найдите время для перерыва. Вам может даже пригодиться быстрый сон; просто держите это меньше 20 минут.
Это может показаться контрпродуктивным, но повышение концентрации внимания, которое дает перерыв, поможет вам достичь гораздо большего, чем если бы вы просто пытались проработать самую низкую точку своего дня.
Если вы хотите узнать больше о том, как время влияет практически на все аспекты вашей жизни, посмотрите When для себя. То, что мы здесь рассмотрели, — всего лишь капля в океане чрезвычайно полезной информации, которую Пинк предоставляет в своей книге. Используйте его, чтобы создать план действий по повышению производительности и принятию более эффективных решений во всех аспектах личной и профессиональной жизни.
Цена: Когда: Научные секреты идеального времени доступен на Amazon по цене от 14,99 долларов США на Kindle, 17,42 доллара США в твердой обложке или 20,40 долларов США в мягкой обложке.
Заглавная фотография сделана jarmoluk через Pixabay. «Часы» от jarmoluk через Pixabay. Диаграммы «Пик, впадина и отскок» и «Идентификация хронотипа» из Когда: Научные секреты идеального времени .

 Свода знаний по управлению проектами (PMBOK) Область знаний по управлению содержит следующие 6 процессов:
Свода знаний по управлению проектами (PMBOK) Область знаний по управлению содержит следующие 6 процессов: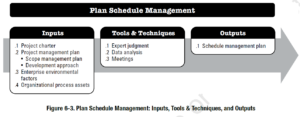 План управления проектом
План управления проектом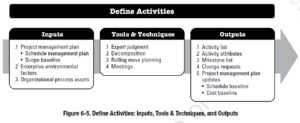 Входы
Входы 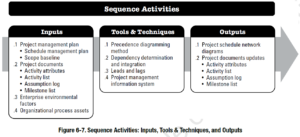 Входы
Входы 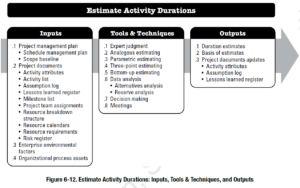 Входы
Входы 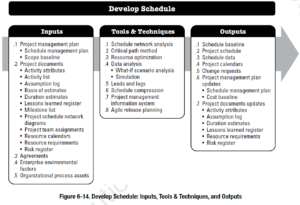 Входы
Входы 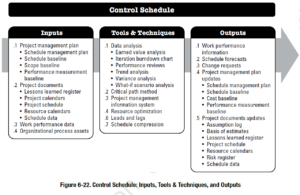 Входы
Входы