Построение и решение графиков Функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
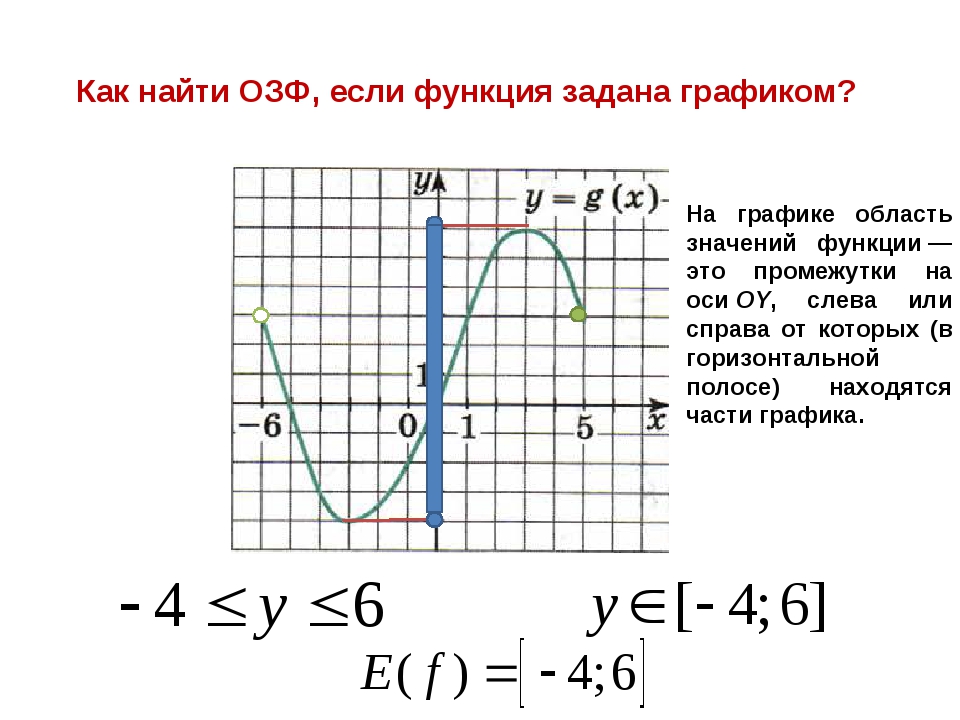
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.

- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».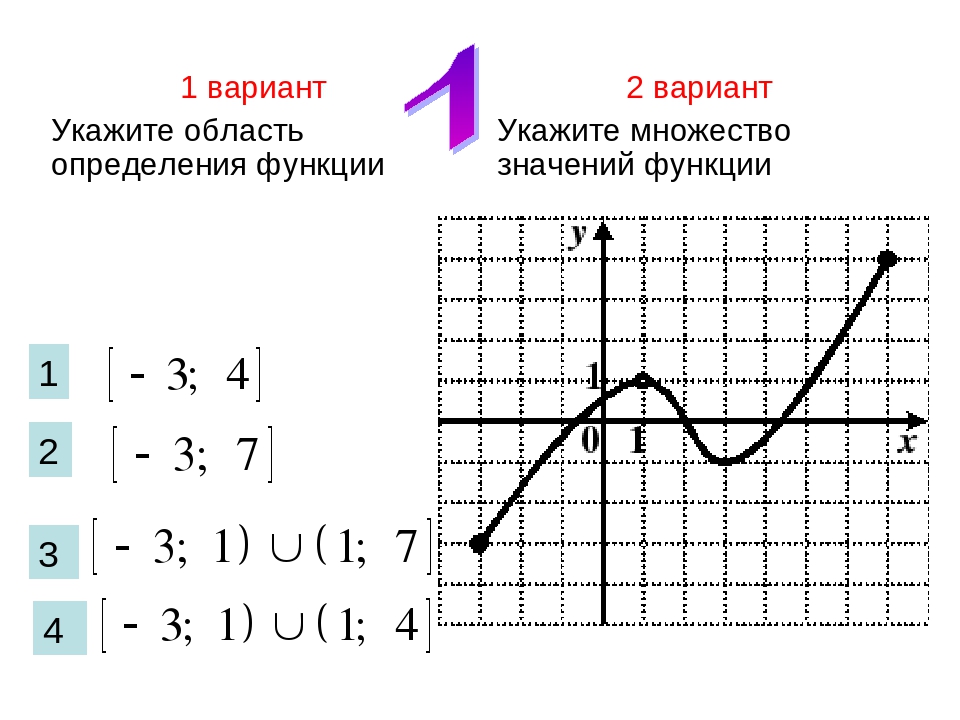
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Как решаем:
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.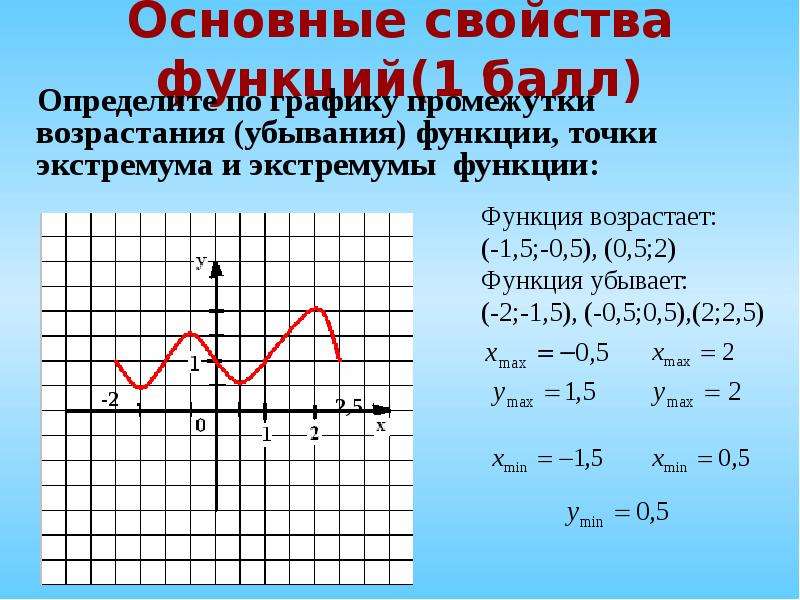
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
y = √x
Сдвигаем график вправо на 1:
y = √x — 1
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.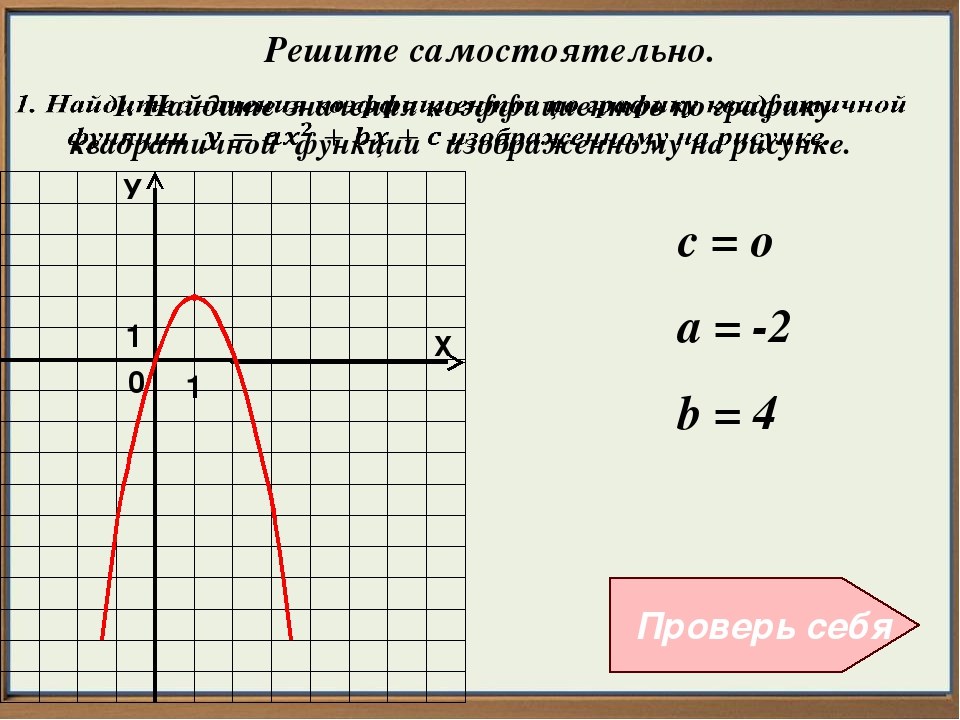
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Линейная функция, график — прямая. Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты
Тестирование онлайн
Линейная функция
Определение. График
Линейной функцией называется функция вида
где k, b — некоторые числа.
Функция вида называется прямой пропорциональностью, является частным случаем линейной зависимости.
Графиком линейной функции является прямая линия.
Для построения графика достаточно знать координаты двух точек.
Свойства линейной функции
1) Область определения функции — множество всех действительных чисел
2) Множеством значений функции является множество всех действительных чисел
3) Функция не имеет ни наибольшего, ни наименьшего значений.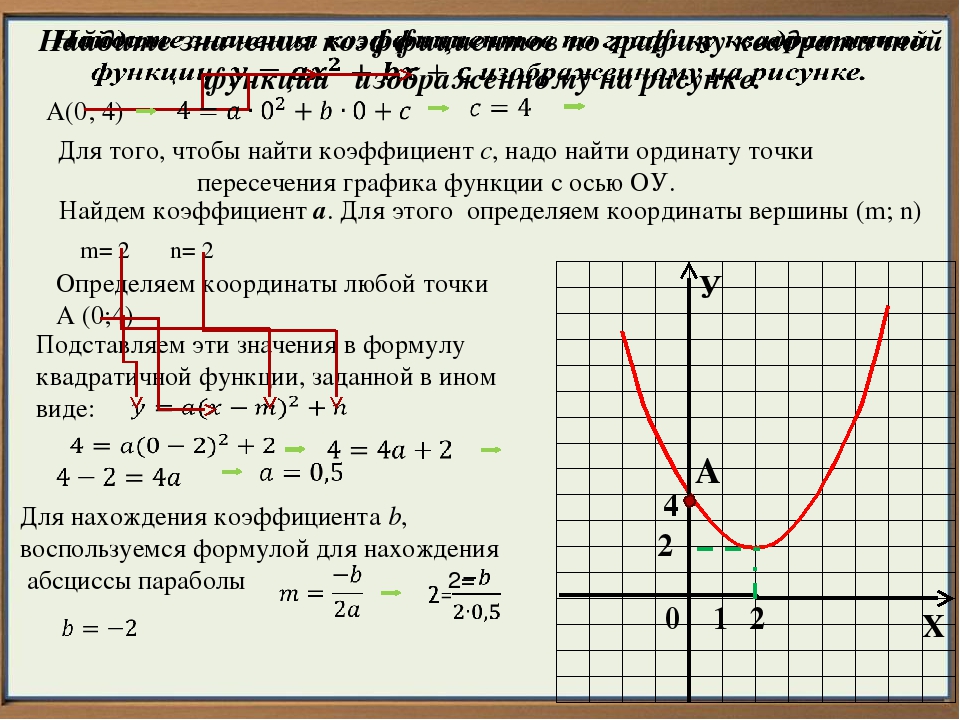
4) Функция не является ни четной, ни нечетной (кроме особых случаев).
5) Функция непериодическая.
6) График функции пересекает ось Ох в точке , а ось Оу — в точке (0; b).
7) — является нулем функции.
8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k.
9) При k>0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
При k: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
10) Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом. Если k>0, то этот угол острый, если k — тупой, если k=0, то прямая совпадает с осью Ох.
Для построения графика функции — прямой линии, очевидно, достаточно двух точек.
Особые случаи
1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.
Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.
2) Если k=0, получим уравнение y=b. Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).
Определить графику в зависимости от определений функций свойство в формах
Вы находитесь здесь:Справка EPLAN > Управление основными данными > Редактор форм и рамок > Процесс работы > Определить графику в зависимости от определений функций свойство в формах
Свойство Присвоение определения функции графике требуется, чтобы различная графика могла размещаться в зависимости от конкретных значений определения , например, для клемм в зависимости от типа клемм.
Условия:
- Вы открыли проект.
- В редакторе форм открыта та форма, которой требуется обработать (Сервисные программы > Основные данные > Форма > Открыть > [Открыть]).

- Открыто диалоговое окно Свойства формы — <Имя формы> (Всплывающее меню > Свойства на форме в диалоговом окне навигатора Страницы — <Имя проекта>).
- В диалоговом окне Свойства формы — <Имя формы> щелкните кнопку […] в столбце Значение свойства Присвоение определения функции графике.
- В диалоговом окне Присвоение определения функции графике щелкните (Создать), чтобы новую строку в таблице присвоений.
- В поле Определение функции щелкните по кнопке […].
- В диалоговом окне Определения функции выберите определение функции, которому Вы хотите присвоить графику.
- Щелкните по кнопке [OK].
Соответствующие данные будут скопированы в поля Категория, Группа и Описание.
- В поле Имя символа щелкните по кнопке […].
- Выберите в диалоговом окне Выбор символов символ, графику которого вы хотите присвоить определению функции.

- Щелкните по кнопке [OK].
Соответствующие данные будут применены в полях Библиотека символов и Описание.
- В поле Вариант символа выберите требуемый вариант из раскрывающегося списка всех имеющихся вариантов текущего символа.
- Выполните аналогичные для всех других присвоений.
- Щелкните по кнопке [OK].
Присвоения сохраняются и могут быть вставлены с помощью заполнителей в форме.
В диалоговом окне Свойства формы — <Имя формы> присвоения выводятся в столбце Значение следующим образом:
<Категория>;<Группа>;<Определение функции>; <Библиотека символов>;<Номер символа>;<Вариант>|
<Категория>;<Группа>;<Определение функции>; <Библиотека символов>;<Номер символа>;<Вариант>|…
Замечание:
Обратите внимание на то, что на просмотр выводятся только символы сохраненных библиотек символов.
См. также
Вставить графику форм
Как определить по функции какой будет график. Функции и графики
функция — это соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества.
график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:
точка располагается (или находится) на графике функции тогда и только тогда, когда .
Таким образом, функция может быть адекватно описана своим графиком.
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Это приводит к следующему способу задания функции.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.
Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и qпринадлежит интервалу = r. Функция E(x) = [x] постоянна на промежутке = r.
Пример 2: функция y = {x} — дробная часть числа. Точнее y ={x} = x — [x], где [x] — целая часть числа x. Эта функция определена для всех x. Если x — произвольное число, то представив его в виде x = r + q (r = [x]), где r — целое число и q лежит в интервале .
Мы видим,что добавление n к аргументу x, не меняет значение функции.
Наименьшее отличное от нуля число из n есть , таким образом, это период sin 2x .
Значение аргумента, при котором функция равна 0, называется нулём (корнем ) функции.
Функция может иметь несколько нулей.
Например, функция y = x (x + 1)(x-3) имеет три нуля: x = 0, x = — 1, x =3 .
Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .
На рис.7 представлен график функции с нулями: x = a, x = b и x = c .
Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой .
Обратная функция
Пусть задана функция у=ƒ(х) с областью определения D и множеством значений Е. Если каждому значению уєЕ соответствует единственное значение хєD, то определена функция х=φ(у) с областью определения Е и множеством значений D (см. рис. 102).
Такая функция φ(у) называется обратной к функции ƒ(х) и записывается в следующем виде: х=j(y)=f -1 (y). Про функции у=ƒ(х) и х=φ(у) говорят, что они являются взаимно обратными. Чтобы найти функцию х=φ(у), обратную к функции у=ƒ (х), достаточно решить уравнение ƒ(х)=у относительно х (если это возможно).
Про функции у=ƒ(х) и х=φ(у) говорят, что они являются взаимно обратными. Чтобы найти функцию х=φ(у), обратную к функции у=ƒ (х), достаточно решить уравнение ƒ(х)=у относительно х (если это возможно).
1. Для функции у=2х обратной функцией является функция х=у/2;
2.Для функции у=х2 хє обратной функцией является х=√у; заметим, что для функции у=х 2 , заданной на отрезке [-1; 1], обратной не существует, т. к. одному значению у соответствует два значения х (так, если у=1/4, то х1=1/2, х2=-1/2).
Из определения обратной функции вытекает, что функция у=ƒ(х) имеет обратную тогда и только тогда, когда функция ƒ(х) задает взаимно однозначное соответствие между множествами D и Е. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Заметим, что функция у=ƒ(х) и обратная ей х=φ(у) изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через х, а зависимую переменную через у, то функция обратная функции у=ƒ(х) запишется в виде у=φ(х).
е. аргумент) обозначить через х, а зависимую переменную через у, то функция обратная функции у=ƒ(х) запишется в виде у=φ(х).
Это означает, что точка M 1 (x o ;y o) кривой у=ƒ(х) становится точкой М 2 (у о;х о) кривой у=φ(х). Но точки M 1 и М 2 симметричны относительно прямой у=х (см. рис. 103). Поэтому графики взаимно обратных функции у=ƒ(х) и у=φ(х) симметричны относительно биссектрисы первого и третьего координатных углов.
Сложная функция
Пусть функция у=ƒ(u) определена на множестве D, а функция u= φ(х) на множестве D 1 , причем для x D 1 соответствующее значение u=φ(х) є D. Тогда на множестве D 1 определена функция u=ƒ(φ(х)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции).
Переменную u=φ(х) называют промежуточным аргументом сложной функции.
Например, функция у=sin2x есть суперпозиция двух функций у=sinu и u=2х. Сложная функция может иметь несколько промежуточных аргументов.
4. Основные элементарный функции и их графики.
Основными элементарными функциями называют следующие функции.
1) Показательная функция у=a х,a>0, а ≠ 1. На рис. 104 показаны графики показательных функций, соответствующие различным основаниям степени.
2) Степенная функция у=х α , αєR. Примеры графиков степенных функций, соответствующих различным показателям степени, предоставлены на рисунках
3)Логарифмическая функция y=log a x, a>0,a≠1;Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 106.
4) Тригонометрические функции у=sinx, у=cosx, у=tgх, у=ctgx; Графики тригонометрических функций имеют вид, показанный на рис. 107.
5) Обратные тригонометрические функции у=arcsinx, у=arccosх, у=arctgx, у=arcctgx. На рис. 108 показаны графики обратных тригонометрических функций.
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называется элементарной функцией.
Примерами элементарных функций могут служить функции
Примерами неэлементарных функций могут служить функции
5. Понятия предела последовательности и функции. Свойства пределов.
Преде́л фу́нкции (предельное значение функции ) в заданной точке,предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.
В математике пределом последовательности элементов метрического пространства или топологического пространства называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементовтопологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. В метрическом пространстве окрестности определяются через функцию расстояния, поэтому понятие предела формулируется на языке расстояний. Исторически первым было понятиепредела числовой последовательности, возникающее в математическом анализе, где оно служит основанием для системы приближений и широко используется при построении дифференциального и интегральногоисчислений.
Исторически первым было понятиепредела числовой последовательности, возникающее в математическом анализе, где оно служит основанием для системы приближений и широко используется при построении дифференциального и интегральногоисчислений.
Обозначение:
(читается: предел последовательности икс-энное при эн, стремящемся к бесконечности, равен a )
Свойство последовательности иметь предел называют сходимостью : если у последовательности есть предел, то говорят, что данная последовательность сходится ; в противном случае (если у последовательности нет предела) говорят, что последовательность расходится . В хаусдорфовом пространстве и, в частности, метрическом пространстве , каждая подпоследовательность сходящейся последовательности сходится, и её предел совпадает с пределом исходной последовательности. Другими словами, у последовательности элементов хаусдорфово пространства не может быть двух различных пределов. Может, однако, оказаться, что у последовательности нет предела, но существует подпоследовательность (данной последовательности), которая предел имеет. Если из любой последовательности точек пространства можно выделить сходящуюся подпоследовательность, то, говорят, что данное пространство обладает свойством секвенциальной компактности (или, просто, компактности, если компактность определяется исключительно в терминах последовательностей).
Если из любой последовательности точек пространства можно выделить сходящуюся подпоследовательность, то, говорят, что данное пространство обладает свойством секвенциальной компактности (или, просто, компактности, если компактность определяется исключительно в терминах последовательностей).
Понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке.
Определение
Пусть дано топологическое пространство и последовательность Тогда, если существует элемент такой, что
где — открытое множество, содержащее , то он называется пределом последовательности . Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент такой, что
где — метрика, то называется пределом .
· Если пространство снабжено антидискретной топологией, то пределом любой последовательности будет любой элемент пространства.
6. Предел функции в точке. Односторонние пределы.
Функция одной переменной. Определение предела функции в точке по Коши. Число b называется пределом функции у = f (x ) при х , стремящемся к а (или в точке а ), если для любого положительного числа существует такое положительное число , что при всех х ≠ а, таких, что |x – a | | f (x ) – a |
Определение предела функции в точке по Гейне. Число b называется пределом функции у = f (x ) при х , стремящемся к а (или в точке а ), если для любой последовательности {x n }, сходящейся к а (стремящейся к а , имеющей пределом число а ), причем ни при каком значении n х n ≠ а , последовательность {y n = f (x n)} сходится к b .
Данные определения предполагают, что функция у = f (x ) определена в некоторой окрестноститочки а , кроме, быть может, самой точки а .
Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму.
Указанный предел обозначается так:
Геометрически существование предела функции в точке по Коши означает, что для любого числа > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2 > 0, высотой 2 и центром в точке (а; b ), что все точки графика данной функции на интервале (а – ; а + ), за исключением, быть может, точки М (а ; f (а )), лежат в этом прямоугольнике
Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва ) и правосторо́нним преде́лом (преде́лом спра́ва ). Пусть на некотором числовом множестве задана числовая функция и число — предельная точка области определения . Существуют различные определения для односторонних пределов функции в точке , но все они эквивалентны.
Существуют различные определения для односторонних пределов функции в точке , но все они эквивалентны.
1) Область определения функции и область значений функции .
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена. Область значений функции — это множество всех действительных значений y , которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции .
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции .
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции .
Возрастающая
функция (в некотором промежутке) —
функция, у которой большему значению
аргумента из этого промежутка
соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции .
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x ). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции .
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7)
Периодическость функции .
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
19. Основные элементарные функции, их свойства и графики. Применение функ-ций в экономике.
Основные элементарные функции. Их свойства и графики
1. Линейная функция.
Линейной функцией называется функция вида , где х — переменная, а и b — действительные числа.
Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.
Свойства линейной функции
1. Область определения — множество всех действительных чисел: Д(y)=R
2. Множество значений — множество всех действительных чисел: Е(у)=R
3. Функция принимает
нулевое значение при
или.
Функция принимает
нулевое значение при
или.
4. Функция возрастает (убывает) на всей области определения.
5. Линейная функция непрерывная на всей области определения, дифференцируемая и .
2. Квадратичная функция.
Функция вида , где х — переменная, коэффициенты а, b, с — действительные числа, называетсяквадратичной.
Степенная функция. Это
функция: y =
ax
n ,
где a, n – постоянные. При n = 1 получаем прямую пропорциональность : y = ax ;
при n = 2 — квадратную параболу ;
при n =
—
1
— обратную пропорциональность или гиперболу . Таким
образом,
эти
функции
—
частные
случаи
степенной
функции.
Мы
знаем,
что
нулевая
степень
любого
числа,
отличного
от
нуля,
равна
1, cледовательно, приn = 0 степенная функция
превращается в постоянную величину: y = a ,
т.
e
.
её
график
—
прямая линия,
параллельная оси Х ,
исключая начало координат (поясните, пожалуйста,
почему
?
). Все эти
случаи (при a =
1 )
показаны на рис.13 (n 0
) и рис.14 ( n x здесь не рассматриваются, так как тогда некоторые функции:
Все эти
случаи (при a =
1 )
показаны на рис.13 (n 0
) и рис.14 ( n x здесь не рассматриваются, так как тогда некоторые функции:
Если n – целые, степенные функции имеют смысл и при x n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
При n =
2 функция чётная и
её график симметричен
относительно
оси Y . При n = 3 функция нечётная и её график симметричен относительно начала
координат. Функция y = x 3 называется кубической параболой .
На рис.16
представлена
функция
.
Эта функция является обратной к квадратной параболе y = x 2 ,
её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла
.
Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим
по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике,
поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.
Мы видим
по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике,
поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.
Что означают слова «задать функцию»? Они означают: объяснить всем желающим, о какой конкретной функции идёт речь. Причём, объяснить чётко и однозначно!
Как это можно сделать? Как задать функцию?
Можно написать формулу. Можно нарисовать график. Можно составить табличку. Любой способ — это какое-то правило, по которому можно узнать значение игрека для выбранного нами значения икса. Т.е. «задать функцию» , это значит — показать закон, правило, по которому икс превращается в игрек.
Обычно, в самых различных заданиях присутствуют уже готовые функции. Они нам уже заданы. Решай себе, да решай.) Но… Чаще всего школьники (да и студенты) работают с формулами. Привыкают, понимаешь. .. Так привыкают, что любой элементарный вопрос, относящийся к другому способу задания функции, тотчас огорчает человека…)
.. Так привыкают, что любой элементарный вопрос, относящийся к другому способу задания функции, тотчас огорчает человека…)
Во избежание подобных случаев, имеет смысл разобраться с разными способами задания функций. Ну и, конечно, применить эти знания к «хитрым» вопросам. Это достаточно просто. Если знаете, что такое функция…)
Поехали?)
Аналитический способ задания функции.
Самый универсальный и могучий способ. Функция, заданная аналитически, это функция, которая задана формулами. Собственно, это и есть всё объяснение.) Знакомые всем (хочется верить!)) функции, например: y = 2x, или y = x 2 и т.д. и т.п. заданы именно аналитически.
К слову сказать, не всякая формула может задавать функцию. Не в каждой формуле соблюдается жёсткое условие из определения функции. А именно — на каждый икс может быть только один игрек. Например, в формуле у = ±х , для одного значения х=2, получается два значения у: +2 и -2. Нельзя этой формулой задать однозначную функцию. А с многозначными функциями в этом разделе математики, в матанализе, не работают, как правило.
Нельзя этой формулой задать однозначную функцию. А с многозначными функциями в этом разделе математики, в матанализе, не работают, как правило.
Чем хорош аналитический способ задания функции? Тем, что если у вас есть формула — вы знаете про функцию всё! Вы можете составить табличку. Построить график. Исследовать эту функцию по полной программе. Точно предсказать, где и как будет вести себя эта функция. Весь матанализ стоит именно на таком способе задания функций. Скажем, взять производную от таблицы крайне затруднительно…)
Аналитический способ достаточно привычен и проблем не создаёт. Разве что некоторые разновидности этого способа, с которыми сталкиваются студенты. Я про параметрическое и неявное задание функций.) Но такие функции — в специальном уроке.
Переходим к менее привычным способам задания функции.
Табличный способ задания функции.
Как следует из названия, этот способ представляет собой простую табличку. В этой таблице каждому иксу соответствует (ставится в соответствие ) какое-то значение игрека. В первой строчке — значения аргумента. Во второй строчке — соответствующие им значения функции, например:
В первой строчке — значения аргумента. Во второй строчке — соответствующие им значения функции, например:
Таблица 1.
| x | — 3 | — 1 | 0 | 2 | 3 | 4 |
| y | 5 | 2 | — 4 | — 1 | 6 | 5 |
Прошу обратить внимание! В данном примере игрек зависит от икса как попало. Я специально так придумал.) Нет никакой закономерности. Ничего страшного, так бывает. Значит, именно так я задал эту конкретную функцию. Именно так я установил правило, по которому икс превращается в игрек.
Можно составить другую табличку, в которой будет закономерность. Этой табличкой будет задана другая функция, например:
Этой табличкой будет задана другая функция, например:
Таблица 2.
| x | — 3 | — 1 | 0 | 2 | 3 | 4 |
| y | — 6 | — 2 | 0 | 4 | 6 | 8 |
Уловили закономерность? Здесь все значения игрека получаются умножением икса на двойку. Вот и первый «хитрый» вопрос: можно ли функцию, заданную с помощью Таблицы 2, считать функцией у = 2х ? Подумайте пока, ответ будет ниже, в графическом способе. Там это всё очень наглядно.)
Чем хорош табличный способ задания функции? Да тем, что считать ничего не надо. Всё уже посчитано и написано в таблице.) А более ничего хорошего нет. Мы не знаем значения функции для иксов, которых нет в таблице. В этом способе такие значения икса просто не существуют. Кстати, это подсказка к хитрому вопросу.) Мы не можем узнать, как ведёт себя функция за пределами таблицы. Ничего не можем. Да и наглядность в этом способе оставляет желать лучшего… Для наглядности хорош графический способ.
Мы не знаем значения функции для иксов, которых нет в таблице. В этом способе такие значения икса просто не существуют. Кстати, это подсказка к хитрому вопросу.) Мы не можем узнать, как ведёт себя функция за пределами таблицы. Ничего не можем. Да и наглядность в этом способе оставляет желать лучшего… Для наглядности хорош графический способ.
Графический способ задания функции.
В данном способе функция представлена графиком. По оси абсцисс откладывается аргумент (х), а по оси ординат — значение функции (у). По графику тоже можно выбрать любой х и найти соответствующее ему значение у . График может быть любой, но… не какой попало.) Мы работаем только с однозначными функциями. В определении такой функции чётко сказано: каждому х ставится в соответствие единственный у . Один игрек, а не два, или три… Для примера, посмотрим на график окружности:
Окружность, как окружность… Почему бы ей не быть графиком функции? А давайте найдем, какой игрек будет соответствовать значению икса, например, 6? Наводим курсор на график (или касаемся рисунка на планшете), и. .. видим, что этому иксу соответствует два значения игрека: у=2 и у=6.
.. видим, что этому иксу соответствует два значения игрека: у=2 и у=6.
Два и шесть! Стало быть, такой график не будет графическим заданием функции. На один икс приходится два игрека. Не соответствует этот график определению функции.
Но если условие однозначности выполнено, график может быть совершенно любым. Например:
Эта самая кривулина — и есть закон, по которому можно перевести икс в игрек. Однозначный. Захотелось нам узнать значение функции для х = 4, например. Надо найти четвёрку на оси иксов и посмотреть, какой игрек соответствует этому иксу. Наводим мышку на рисунок и видим, что значение функции у для х=4 равно пяти. Какой формулой задано такое превращение икса в игрек — мы не знаем. И не надо. Графиком всё задано.
Теперь можно вернуться к «хитрому» вопросу про у=2х. Построим график этой функции. Вот он:
Разумеется, при рисовании этого графика мы не брали бесконечное множество значений х.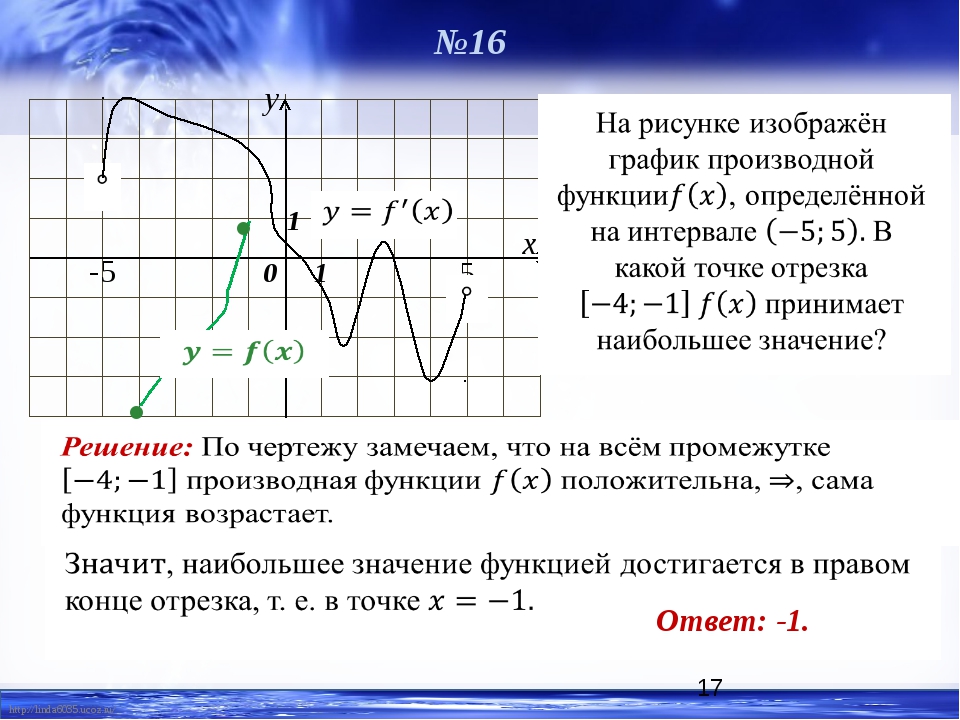 Взяли несколько значений, посчитали у, составили табличку — и всё готово! Самые грамотные вообще всего два значения икса взяли! И правильно. Для прямой больше и не надо. Зачем лишняя работа?
Взяли несколько значений, посчитали у, составили табличку — и всё готово! Самые грамотные вообще всего два значения икса взяли! И правильно. Для прямой больше и не надо. Зачем лишняя работа?
Но мы совершенно точно знали, что икс может быть любым. Целым, дробным, отрицательным… Любым. Это по формуле у=2х видно. Поэтому смело соединили точки на графике сплошной линией.
Если же функция будет нам задана Таблицей 2, то значения икса нам придётся брать только из таблицы. Ибо другие иксы (и игреки) нам не даны, и взять их негде. Нет их, этих значений, в данной функции. График получится из точек. Наводим мышку на рисунок и видим график функции, заданной Таблицей 2. Значения икс-игрек на осях я не писал, разберётесь, поди, по клеточкам?)
Вот и ответ на «хитрый» вопрос. Функция, заданная Таблицей 2 и функция у=2х — разные.
Графический способ хорош своей наглядностью. Сразу видно, как ведёт себя функция, где возрастает.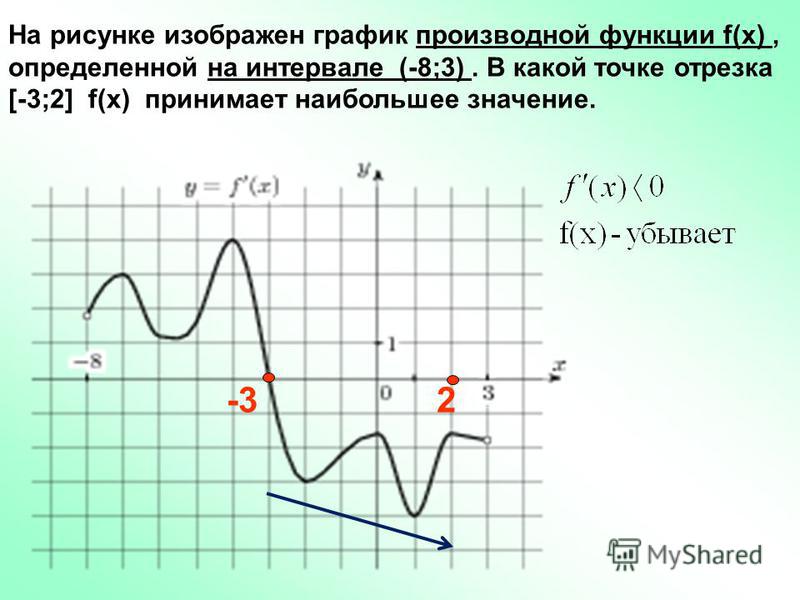 где убывает. По графику сразу можно узнать некоторые важные характеристики функции. А уж в теме с производной, задания с графиками — сплошь и рядом!
где убывает. По графику сразу можно узнать некоторые важные характеристики функции. А уж в теме с производной, задания с графиками — сплошь и рядом!
Вообще, аналитический и графический способы задания функции идут рука об руку. Работа с формулой помогает построить график. А график частенько подсказывает решения, которые в формуле и не заметишь… Мы с графиками дружить будем.)
Почти любой ученик знает три способа задания функции, которые мы только что рассмотрели. Но на вопрос: «А четвёртый!?» — зависает основательно.)
Такой способ есть.
Словесное описание функции.
Да-да! Функцию можно вполне однозначно задать словами. Великий и могучий русский язык на многое способен!) Скажем, функцию у=2х можно задать следующим словесным описанием: каждому действительному значению аргумента х ставится в соответствие его удвоенное значение. Вот так! Правило установлено, функция задана.
Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно. Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить. И график построить. Кстати, график забавный получается…) Попробуйте.
Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично. А вот табличку легко составить. И график построить. Кстати, график забавный получается…) Попробуйте.
Способ словесного описания — способ достаточно экзотичный. Но иногда встречается. Здесь же я его привёл, чтобы придать вам уверенности в неожиданных и нестандартных ситуациях. Нужно просто понимать смысл слов «функция задана…» Вот он, этот смысл:
Если есть закон однозначного соответствия между х и у — значит, есть функция. Какой закон, в какой форме он выражен — формулой, табличкой, графиком, словами, песнями, плясками — сути дела не меняет. Этот закон позволяет по значению икса определить соответствующее значение игрека. Всё.
Сейчас мы применим эти глубокие знания к некоторым нестандартным заданиям. ) Как и обещано в начале урока.
) Как и обещано в начале урока.
Задание 1:
Функция у = f(x) задана Таблицей 1:
Таблица 1.
Найти значение функции p(4), если p(х)= f(x) — g(x)
Если вы вообще не можете понять, что к чему — прочитайте предыдущий урок «Что такое функция?» Там про такие буковки и скобочки очень понятно написано.) А если вас смущает только табличная форма, то разбираемся здесь.
Из предыдущего урока ясно, что, если, p(х) = f(x) — g(x) , то p(4) = f(4) — g(4) . Буквы f и g означают правила, по которым каждому иксу ставится в соответствие свой игрек. Для каждой буквы (f и g ) — своё правило. Которое задано соответствующей таблицей.
Значение функции f(4) определяем по Таблице 1. Это будет 5. Значение функции g(4) определяем по Таблице 2. Это будет 8. Остаётся самое трудное.)
p(4) = 5 — 8 = -3
Это правильный ответ.
Решить неравенство f(x) > 2
Вот-те раз! Надо решить неравенство, которое (в привычной форме) блистательно отсутствует! Остаётся либо бросать задание, либо включить голову. Выбираем второе и рассуждаем.)
Выбираем второе и рассуждаем.)
Что значит решить неравенство? Это значит, найти все значения икса, при которых выполняется данное нам условие f(x) > 2 . Т.е. все значения функции (у ) должны быть больше двойки. А у нас на графике игрек всякий есть… И больше двойки есть, и меньше… А давайте, для наглядности, по этой двойке границу проведём! Наводим курсор на рисунок и видим эту границу.
Строго говоря, эта граница есть график фукции у=2, но это не суть важно. Важно то, что сейчас на графике очень хорошо видно, где, при каких иксах, значения функции, т.е. у, больше двойки. Они больше при х> 3. При х> 3 вся наша функция проходит выше границы у=2. Вот и всё решение. Но выключать голову ещё рано!) Надо ещё ответ записать…
На графике видно, что наша функция не простирается влево и вправо на бесконечность. Об этом точки на концах графика говорят. Кончается там функция.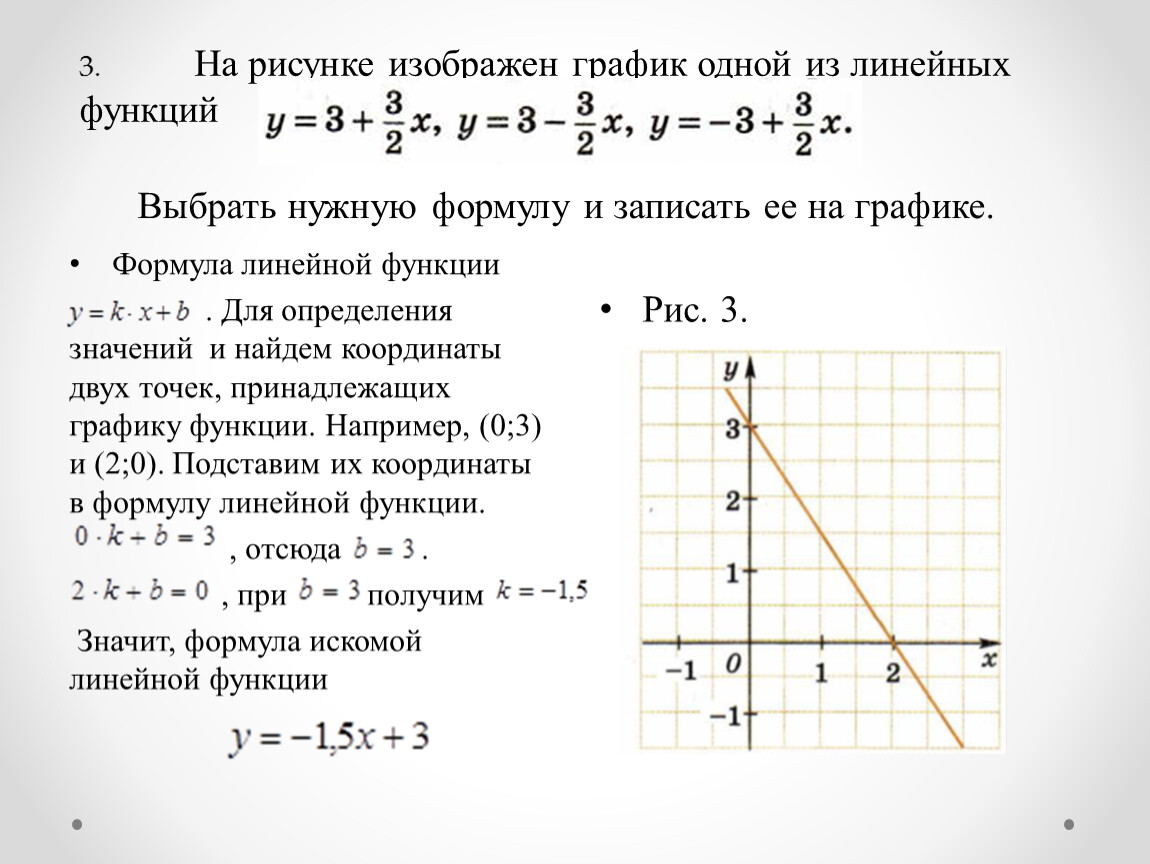 Стало быть, в нашем неравенстве все иксы, которые уходят за пределы функции смысла не имеют. Для функции этих иксов не существует. А мы, вообще-то, неравенство для функции решаем…
Стало быть, в нашем неравенстве все иксы, которые уходят за пределы функции смысла не имеют. Для функции этих иксов не существует. А мы, вообще-то, неравенство для функции решаем…
Правильный ответ будет:
3 х ≤ 6
Или, в другой форме:
х ∈ (3; 6]
Теперь всё, как надо. Тройка не включается в ответ, т.к. исходное неравенство строгое. А шестёрка включается, т.к. и функция при шестёрке существует, и условие неравенства выполняется. Мы успешно решили неравенство, которого (в привычной форме) нету…
Вот так некоторые знания и элементарная логика спасают в нестандартных случаях.)
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f (x ) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у . При этом одно и то же значение у может быть получено при различных х .
Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у . При этом одно и то же значение у может быть получено при различных х .
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х ), при которых функция определена, т.е. ее значение существует. Обозначается область определения D (y ). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е (у ).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f (x ) называют четной х
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f (x ) называют нечетной , если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны.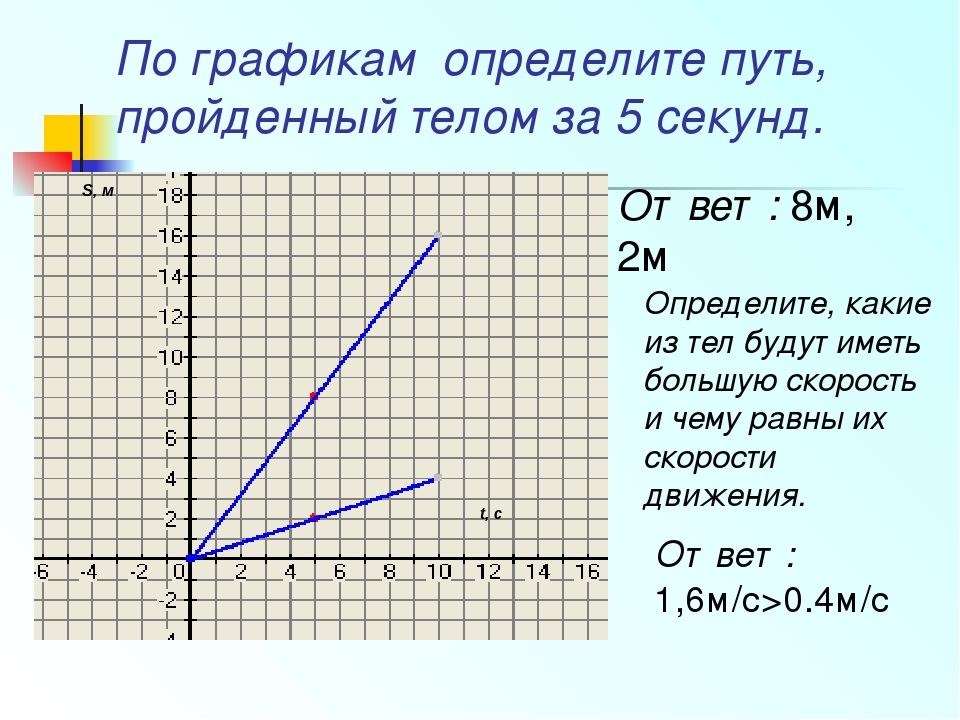 График нечётной функции всегда симметричен относительно начала координат.
График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х .
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида , и для них не выполняется ни одно из равенств или свойств приведенных выше.
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k
График квадратичной функции (Парабола)
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x 1 ; 0) и (x 2 ; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x 0 ; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c ). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x 0 ; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c ). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax 2 + bx + c , то ветви параболы направлены вверх;
- если же a
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a a > 0), значение квадратного трехчлена:
Графики других функций
Степенной функцией
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает.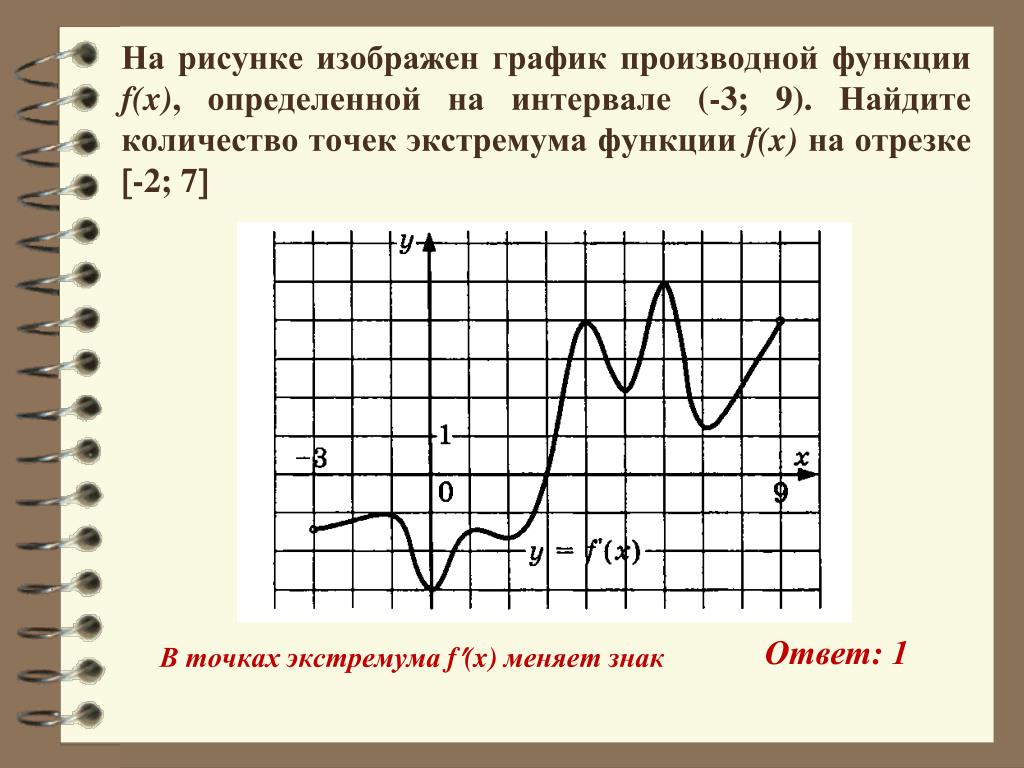 Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x | выглядит следующим образом:
Графики периодических (тригонометрических) функций
Функция у = f (x ) называется периодической , если существует такое, неравное нулю, число Т , что f (x + Т ) = f (x ), для любого х из области определения функции f (x ).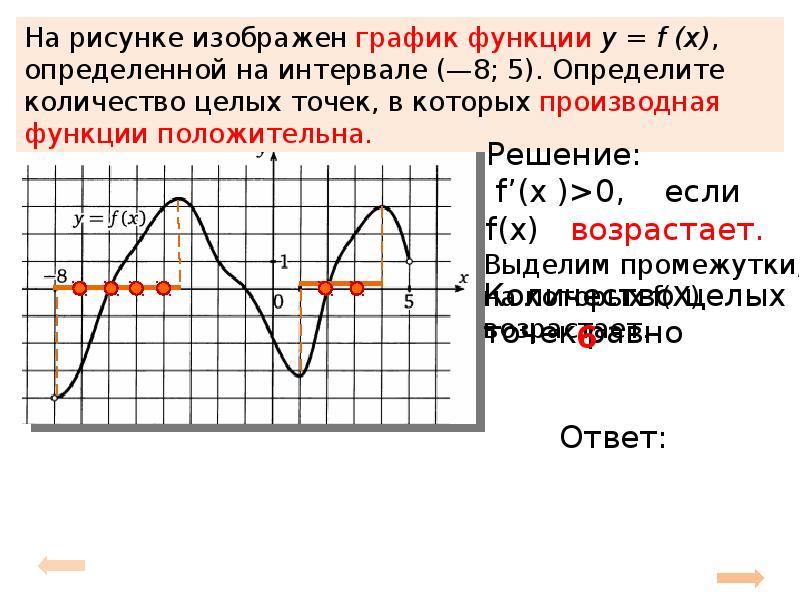 Если функция f (x ) является периодической с периодом T , то функция:
Если функция f (x ) является периодической с периодом T , то функция:
где: A , k , b – постоянные числа, причем k не равно нулю, также периодическая с периодом T 1 , который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой :
График функции y = cosx называется косинусоидой . Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой . Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.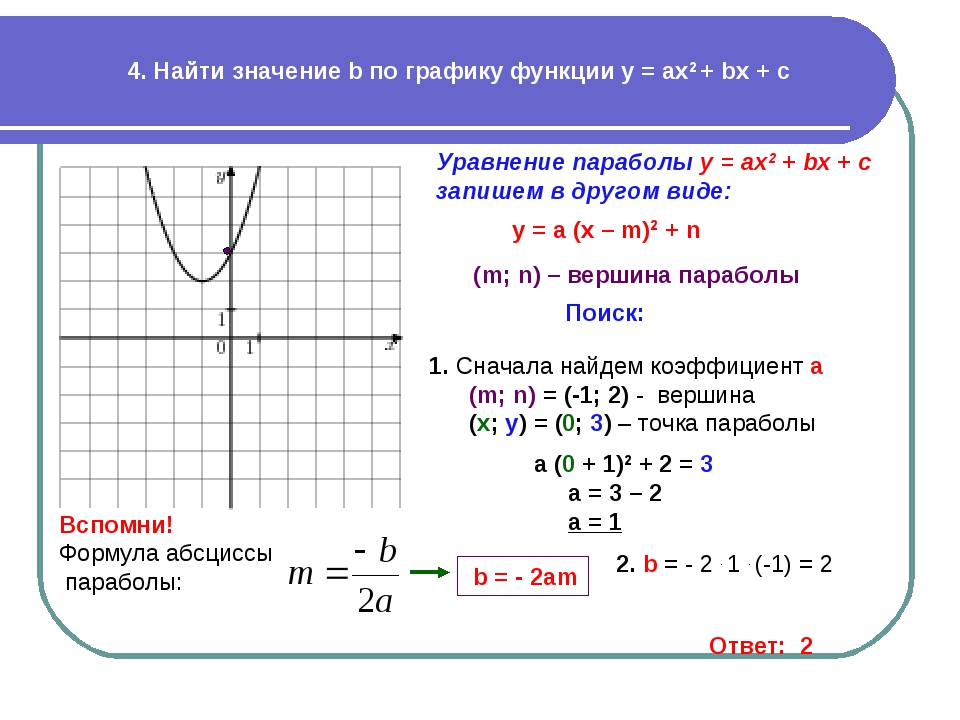
Ну и наконец, график функции y = ctgx называется котангенсоидой . Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
 Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Как научиться читать графики на бирже при торговле акциями
Здравствуйте! Очень хотелось научиться понимать и анализировать движение определенных ценных бумаг с помощью графиков.
Чем различаются разные виды графиков между собой? Что такое японские свечи? А линейный график? Актив один и тот же, а графики очень различаются.
Макс Б.
В торговле на бирже графики нужны для того, чтобы отображать основные параметры цен в удобном визуальном формате. Графики часто используют трейдеры, которые заключают много сделок в рамках одного дня: при активной торговле решение о сделке нужно принимать молниеносно, анализировать данные из таблиц попросту неудобно.
Дмитрий Семин
адепт японских свечей
Но и консервативным инвесторам полезно уметь читать графики: с их помощью инвестор может оценить доходность и поведение актива в прошлом.
Разберем графики на примерах. Возьмем данные из таблицы и представим их на графиках разных видов.
Как менялась цена актива в течение неделиС таблицей все понятно: указаны все важные данные о движении цены. Мы видим, как менялась цена за день: на каком значении торговая сессия началась и на каком закрылась, какого минимального и максимального порога достигла цена за весь день.
Таблицы удобно использовать, когда нужно получить информацию по торгам за конкретный день: в понедельник актив закрылся по цене 55, а в среду — по цене 65. Минус: трудно увидеть тренд — как сильно растет или падает цена актива. Воспринимать направление и изменение цены бумаги по таблице можно, но делать это сложнее, чем по графику.
Линейный график
Такой формат отображения изменений воспринимается глазом проще числовых данных и может визуально показать, что происходило с ценой и как быстро она менялась в течение недели.
По линейному графику удобно отслеживать изменение во времени какого-то одного параметра. В нашей таблице четыре параметра — конечно, можно показать их все на одном графике кривыми разного цвета, но наглядность от этого пострадает. Удобней, когда на графике изображено изменение какого-то одного или двух параметров.
Линейный график: изменение цены закрытияСвечной график
Свечной график — вид графика с дополнительными данными о движении цены за временной период.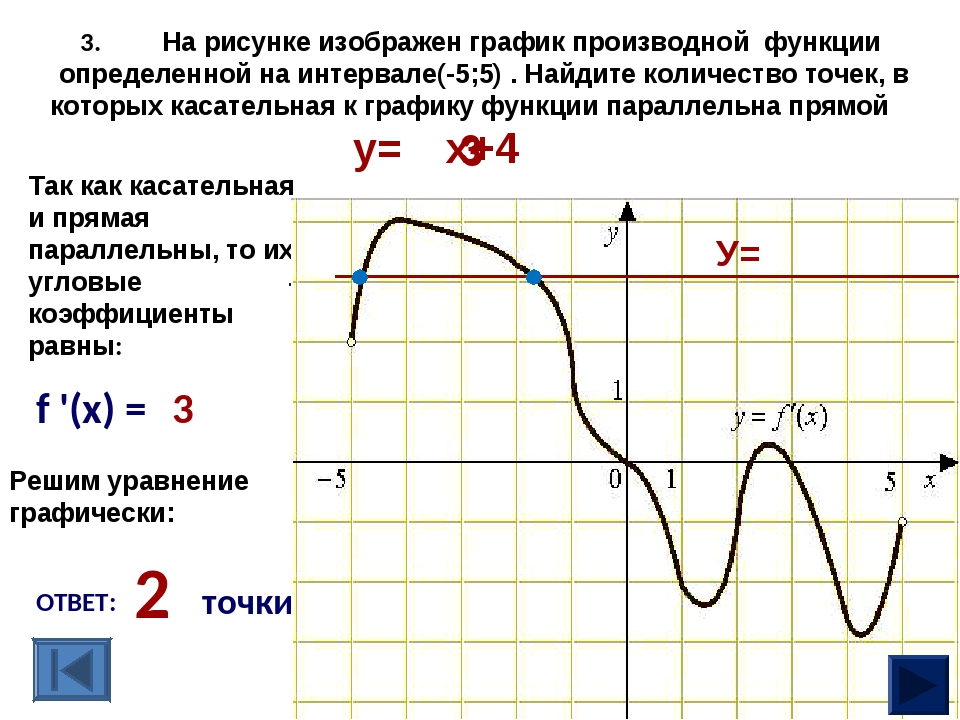 Если на линейном графике мы изобразили только цену закрытия, то на свечном графике видны все данные из таблицы: цена открытия и закрытия торгов, максимальное и минимальное значение цены за торговую сессию.
Если на линейном графике мы изобразили только цену закрытия, то на свечном графике видны все данные из таблицы: цена открытия и закрытия торгов, максимальное и минимальное значение цены за торговую сессию.
В свечах выделяют два основных вида:
- Растущие — если за время формирования свечи цена выросла.
- Падающие — если за время формирования свечи цена снизилась.
Свечу, в которой цены открытия и закрытия совпадают, иногда выделяют в третий тип — дожи, на нашем графике эта свеча тоже есть — в среду.
Стандартно свечи и бары окрашиваются двумя цветами в зависимости от роста или падения цены за промежуток времени. Зеленое тело означает рост цены, а красное — падение. Но удобный цвет свечей или баров всегда можно настроить индивидуально.
Строение японских свечей Японские свечи: по одному графику можно проанализировать сразу все параметры из таблицыБарный график
Барный график показывает те же параметры, что и японские свечи.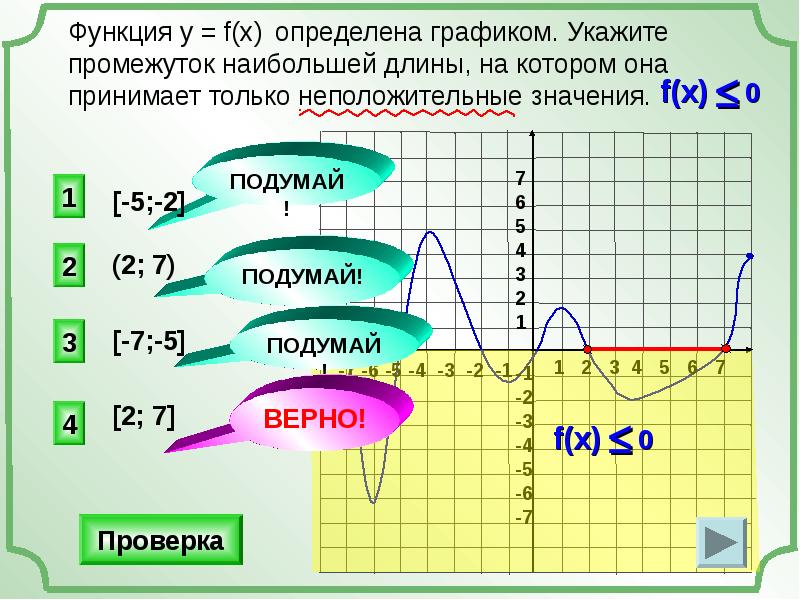 Разница только в отображении.
Разница только в отображении.
Японские свечи выглядят проще для восприятия, но барный график по-прежнему популярен у трейдеров на Западе.
Определить движение цены внутри бара можно по его «ушам» — горизонтальным линиям на его теле. Левым ухом обозначают цену открытия, а правым — цену закрытия бара. Если левое ухо выше правого — цена упала и бар будет красным. Если левое ниже — цена выросла, бар будет зеленым.
Строение баров Барный графикЗачем инвестору нужны графики
Анализ прошлого движения цены по графикам можно использовать, чтобы убедиться, что дела у компании в порядке и рынок подтверждал это ранее. Или как дополнительное подтверждение того, что вы не ошиблись в анализе фундаментальных показателей.
Но вряд ли стоит использовать анализ графиков как единственный фактор для принятия решения об инвестиции своих средств. Для комплексного анализа можно обратить внимание на другие показатели инструмента: риски, доходность, практику и нюансы вложений в конкретный тип актива. Почитайте наши подборки об инвестициях, чтобы разобраться глубже:
Почитайте наши подборки об инвестициях, чтобы разобраться глубже:
Если у вас есть вопрос о личных финансах, правах и законах, здоровье или образовании, пишите. На самые интересные вопросы ответят эксперты журнала.
область определения, нули функции, четность функции и все остальные.
Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.
Графиком функции называют множество всех точек
координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по
оси ординат откладываются значения переменной y. Для
построения графика функции необходимо знать свойства функции.
Основные свойства функции будут рассмотрены далее!
Для
построения графика функции необходимо знать свойства функции.
Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при
которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция — функция, у которой область определения симметрична относительно
начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен
относительно оси ординат.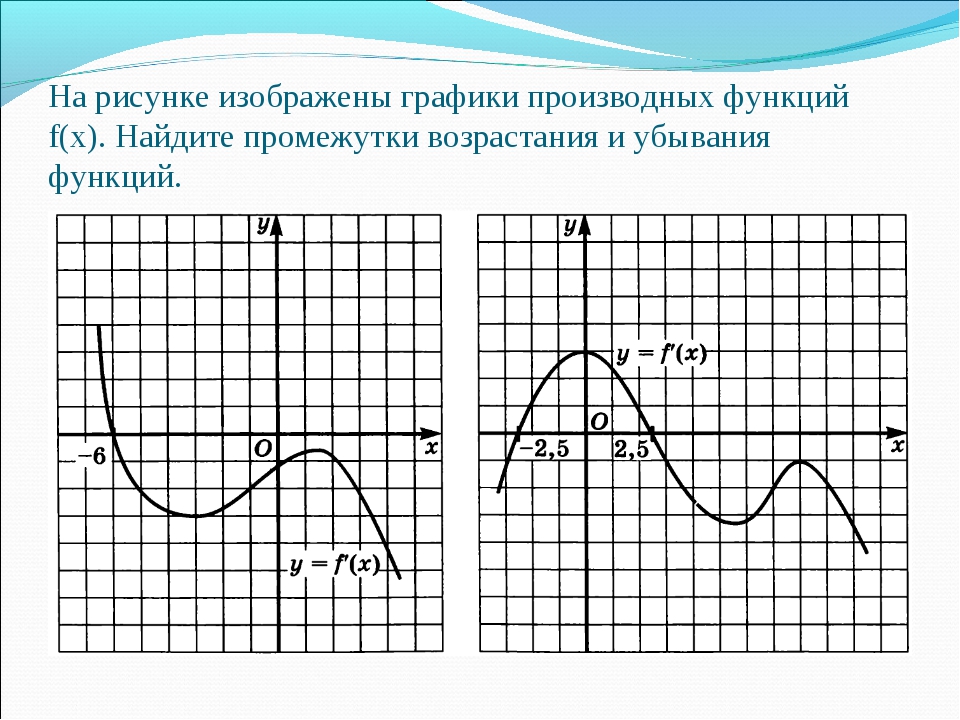
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по
свойствам функции сможете построить график функции.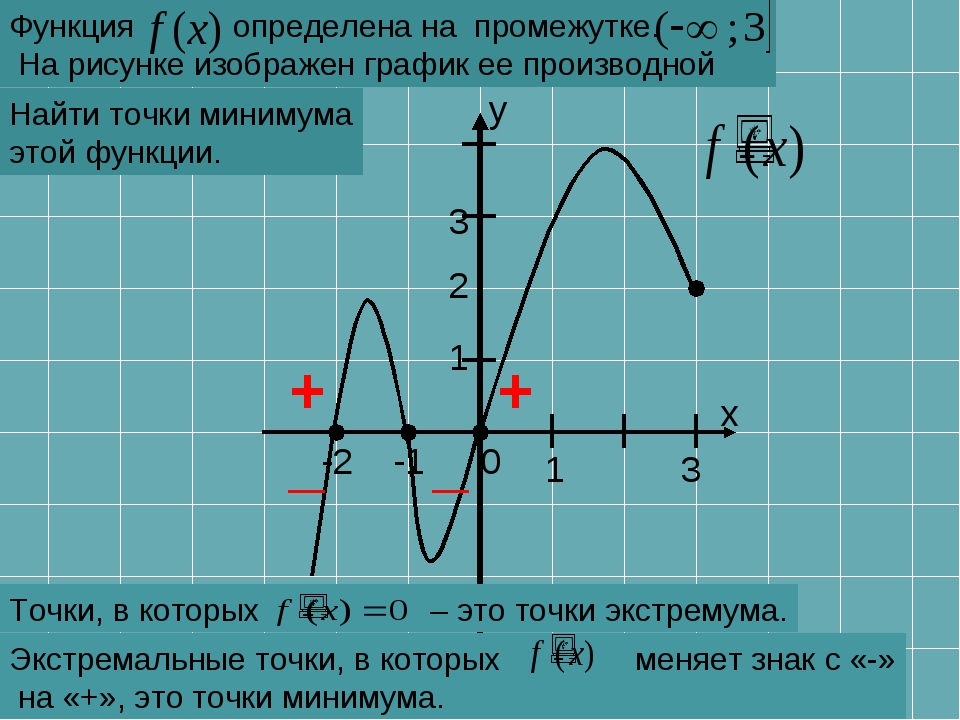 Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.
Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Функции и графики — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Координаты и базовые понятия о функциях
К оглавлению…
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
К оглавлению…
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):
График квадратичной функции (Парабола)
К оглавлению. ..
..
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x0; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Графики других функций
К оглавлению…
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает.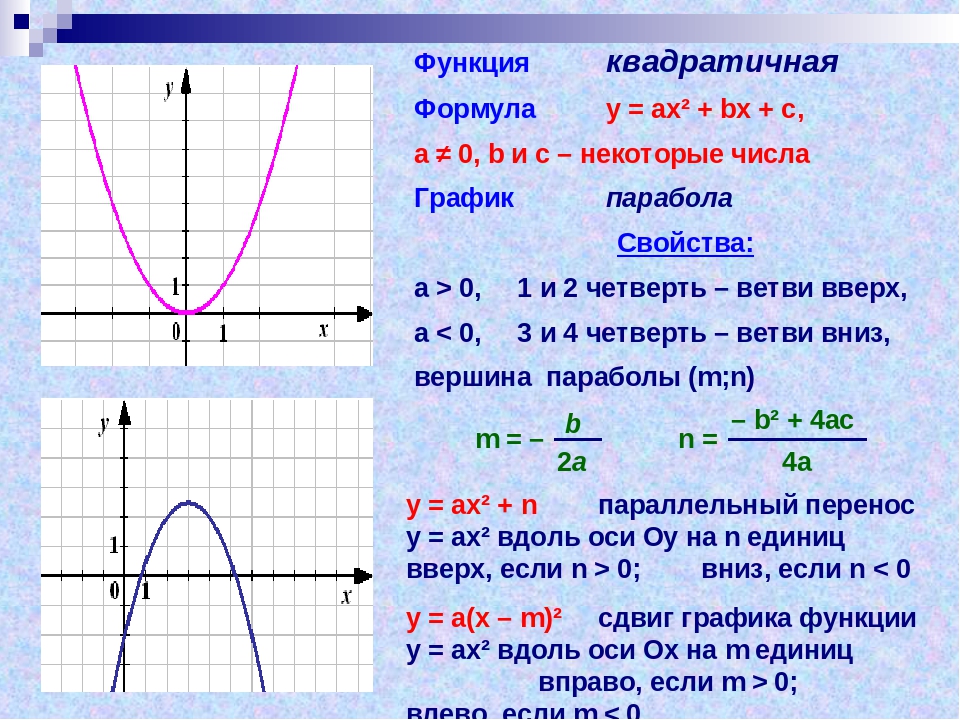 Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x| выглядит следующим образом:
Графики периодических (тригонометрических) функций
К оглавлению…
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x).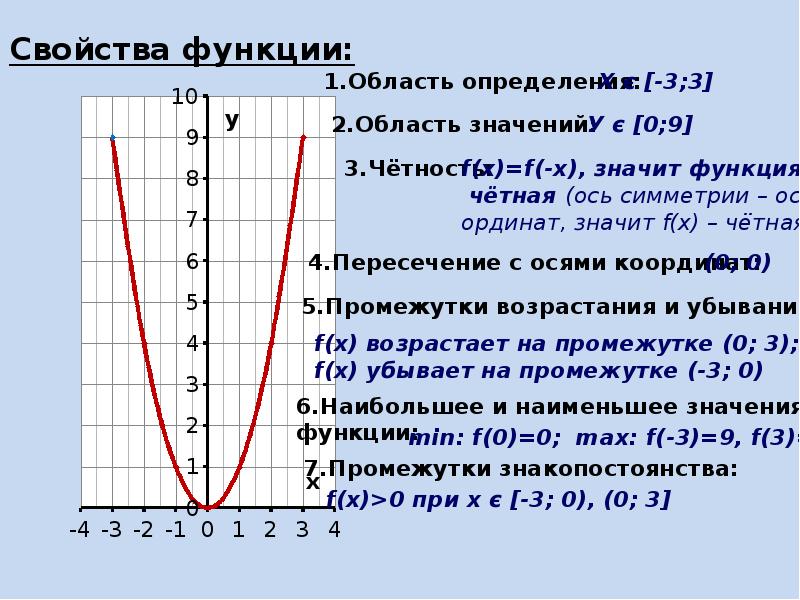 Если функция f(x) является периодической с периодом T, то функция:
Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:
График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Видео: Создание диаграммы
Создайте диаграмму (график), рекомендованную для ваших данных, почти так же быстро, как с помощью мастера диаграмм, который больше не доступен.
Создать диаграмму
Выберите данные, для которых вы хотите создать диаграмму.
Щелкните ВСТАВИТЬ > Рекомендуемые диаграммы .

На вкладке Рекомендуемые диаграммы прокрутите список диаграмм, которые Excel рекомендует для ваших данных, и щелкните любую диаграмму, чтобы увидеть, как будут выглядеть ваши данные.
Если вы не видите понравившуюся диаграмму, щелкните Все диаграммы , чтобы просмотреть все доступные типы диаграмм.
Когда вы найдете понравившуюся диаграмму, щелкните ее > OK .
Используйте кнопки Chart Elements , Chart Styles и Chart Filters , рядом с правым верхним углом диаграммы, чтобы добавить элементы диаграммы, такие как заголовки осей или метки данных, настроить внешний вид диаграммы или изменить данные, представленные на графике.
Чтобы получить доступ к дополнительным функциям дизайна и форматирования, щелкните в любом месте диаграммы, чтобы добавить ИНСТРУМЕНТЫ ДЛЯ ДИАГРАММ на ленту, а затем выберите нужные параметры на вкладках ДИЗАЙН и ФОРМАТ .

Хотите больше?
Скопируйте диаграмму Excel в другую программу Office
Создайте диаграмму от начала до конца
Диаграммыобеспечивают визуальное представление ваших данных, упрощая их анализ.
Например, я хочу создать диаграмму для продаж, чтобы увидеть, есть ли закономерность.
Я выбираю ячейки, которые хочу использовать для диаграммы, нажимаю кнопку Quick Analysis и открываю вкладку CHARTS .
Excel отображает рекомендуемые диаграммы на основе данных в выбранных ячейках.
Вы можете навести курсор на каждый из них, чтобы увидеть, что подходит для ваших данных.
Clustered Column отлично подходит для сравнения данных, поэтому я нажимаю на него.
А теперь у меня есть привлекательная таблица данных.
Похоже, что летние месяцы медленнее, а зимние более загружены.
Далее, Создание круговых, столбчатых и линейных диаграмм .
Как создавать диаграммы и графики в Excel
После ввода данных и выбора диапазона ячеек вы готовы выбрать тип диаграммы для отображения данных. В этом примере мы создадим кластеризованную столбчатую диаграмму из данных, которые мы использовали в предыдущем разделе.
Шаг 1: выберите тип диаграммы
Как только ваши данные будут выделены в рабочей книге, щелкните вкладку «Вставка» в верхнем баннере. Примерно посередине панели инструментов находится раздел с несколькими параметрами диаграммы. Excel предоставляет рекомендуемые диаграммы в зависимости от популярности, но вы можете щелкнуть любое из раскрывающихся меню, чтобы выбрать другой шаблон.
Шаг 2. Создайте свою диаграмму
- На вкладке Вставка щелкните значок гистограммы и выберите Кластеризованный столбец .
- Excel автоматически создаст кластерный столбец диаграммы из выбранных вами данных. Диаграмма появится в центре вашей книги.
- Чтобы назвать вашу диаграмму , дважды щелкните текст Chart Title на диаграмме и введите заголовок. Назовем этот график «Прибыль от продукта 2013–2017».
Мы будем использовать эту диаграмму в оставшейся части прохождения.Вы можете скачать эту же диаграмму, чтобы следовать ей.
Загрузить образец шаблона гистограммы
На панели инструментов есть две вкладки, которые можно использовать для настройки диаграммы: Дизайн диаграммы и Формат . Excel автоматически применяет предустановки дизайна, макета и формата к диаграммам и графикам, но вы можете добавить настройки, изучив вкладки. Далее мы познакомим вас со всеми доступными корректировками в Chart Design .
Excel автоматически применяет предустановки дизайна, макета и формата к диаграммам и графикам, но вы можете добавить настройки, изучив вкладки. Далее мы познакомим вас со всеми доступными корректировками в Chart Design .
Шаг 3. Добавьте элементы диаграммы
Добавление элементов диаграммы на диаграмму или график улучшит их за счет уточнения данных или предоставления дополнительного контекста. Вы можете выбрать элемент диаграммы, щелкнув раскрывающееся меню Добавить элемент диаграммы в верхнем левом углу (под вкладкой Главная ).
Чтобы отобразить или скрыть оси:
- Выберите Оси . Excel автоматически извлечет заголовки столбцов и строк из выбранного диапазона ячеек, чтобы отобразить на диаграмме как горизонтальную, так и вертикальную оси (в разделе Оси есть галочка рядом с Первичная горизонтальная и Первичная вертикальная .
 )
) - Снимите отметку с этих параметров, чтобы удалить ось отображения на диаграмме. В этом примере нажатие кнопки «Основной горизонтальный» удалит метки года на горизонтальной оси диаграммы.
- Нажмите Дополнительные параметры осей … в раскрывающемся меню Оси , чтобы открыть окно с дополнительными параметрами форматирования и текста, такими как добавление делений, меток или чисел, или изменить цвет и размер текста.
Чтобы добавить названия осей:
- Щелкните Добавить элемент диаграммы и щелкните Названия осей в раскрывающемся меню.Excel не будет автоматически добавлять заголовки осей к вашей диаграмме; поэтому Первичный горизонтальный и Первичный вертикальный будут сняты.
- Чтобы создать заголовки осей, нажмите Первичная горизонталь или Первичная вертикаль , и на диаграмме появится текстовое поле.
 Мы нажали оба в этом примере. Введите названия осей. В этом примере мы добавили заголовки «Год» (по горизонтали) и «Прибыль» (по вертикали).
Мы нажали оба в этом примере. Введите названия осей. В этом примере мы добавили заголовки «Год» (по горизонтали) и «Прибыль» (по вертикали).
Чтобы удалить или переместить заголовок диаграммы:
- Щелкните Добавить элемент диаграммы и щелкните Заголовок диаграммы .Вы увидите четыре варианта: Нет, Над диаграммой, Наложение по центру и Дополнительные параметры заголовка .
- Нажмите Нет , чтобы удалить заголовок диаграммы.
- Щелкните Над диаграммой , чтобы поместить заголовок над диаграммой. Если вы создадите заголовок диаграммы, Excel автоматически поместит его над диаграммой.
- Щелкните Наложение по центру , чтобы поместить заголовок в линии сетки диаграммы. Будьте осторожны с этой опцией: вы не хотите, чтобы заголовок перекрывал какие-либо ваши данные или загромождал ваш график (как в примере ниже).
Для добавления меток данных:
- Щелкните Добавить элемент диаграммы и щелкните Метки данных .
 Существует шесть вариантов меток данных: Нет (по умолчанию), Центр, Внутренний конец, Внутреннее основание, Внешний конец, и Дополнительные параметры заголовка метки данных .
Существует шесть вариантов меток данных: Нет (по умолчанию), Центр, Внутренний конец, Внутреннее основание, Внешний конец, и Дополнительные параметры заголовка метки данных . - Четыре варианта размещения добавят определенные метки к каждой точке данных, измеренной на вашей диаграмме. Щелкните нужный вариант.Эта настройка может быть полезна, если у вас мало точных данных или если на диаграмме много свободного места. Однако для гистограммы с кластерами добавление меток данных, скорее всего, будет выглядеть слишком загроможденным. Например, вот как выглядит выбор меток данных Center :
Чтобы добавить таблицу данных:
- Щелкните Добавить элемент диаграммы и щелкните Таблица данных . Существует три предварительно отформатированных параметра, а также расширенное меню, которое можно найти, нажав Дополнительные параметры таблицы данных :
- Нет — это настройка по умолчанию, при которой таблица данных не дублируется на диаграмме.

- С клавишами легенды отображает таблицу данных под диаграммой, чтобы показать диапазон данных. Также будет включена легенда с цветовой кодировкой.
- Ключи без легенды также отображает таблицу данных под диаграммой, но без легенды.
Примечание. Если вы решите включить таблицу данных, вы, вероятно, захотите увеличить размер диаграммы, чтобы вместить таблицу. Просто щелкните угол диаграммы и используйте перетаскивание, чтобы изменить размер диаграммы.
Чтобы добавить планки ошибок:
- Щелкните Добавить элемент диаграммы и щелкните Планки погрешностей . В дополнение к Дополнительные параметры погрешностей есть четыре параметра: Нет (по умолчанию), Стандартная ошибка , 5% (в процентах) и Стандартное отклонение . Добавление планок погрешностей обеспечивает визуальное представление потенциальной ошибки в отображаемых данных на основе различных стандартных уравнений для изоляции ошибки.

- Например, когда мы нажимаем Стандартная ошибка в параметрах, мы получаем диаграмму, похожую на изображение ниже.
Чтобы добавить линии сетки:
- Щелкните Добавить элемент диаграммы и щелкните Линии сетки . В дополнение к Дополнительные параметры линии сетки есть четыре параметра: Основной основной горизонтальный , Основной основной вертикальный , Основной дополнительный горизонтальный и Основной дополнительный вертикальный .Для столбчатой диаграммы Excel по умолчанию добавит 90 104 основных основных горизонтальных 90 105 линий сетки.
- Вы можете выбрать столько различных линий сетки, сколько хотите, щелкая параметры. Например, вот как выглядит наша диаграмма, когда мы нажимаем все четыре варианта линий сетки.
Чтобы добавить легенду:
- Щелкните Добавить элемент диаграммы и щелкните Легенда .
 В дополнение к Дополнительные параметры легенды существует пять вариантов размещения легенды: Нет, Справа, Сверху, Слева и Снизу .
В дополнение к Дополнительные параметры легенды существует пять вариантов размещения легенды: Нет, Справа, Сверху, Слева и Снизу . - Расположение легенды зависит от стиля и формата диаграммы. Отметьте вариант, который лучше всего выглядит на вашем графике. Вот наша диаграмма, когда мы нажимаем на размещение легенды Right .
Для добавления строк: Строки недоступны для столбчатых диаграмм с кластерами. Однако в других типах диаграмм, где вы сравниваете только две переменные, вы можете добавить линии (например, целевую, среднюю, эталонную и т. д.) в свою диаграмму, отметив соответствующую опцию.
Чтобы добавить линию тренда:
- Щелкните Добавить элемент диаграммы и щелкните Линия тренда . В дополнение к Дополнительные параметры линии тренда есть пять параметров: Нет (по умолчанию), Линейный, Экспоненциальный, Линейный прогноз, и Скользящее среднее .
 Отметьте подходящий вариант для вашего набора данных. В этом примере мы нажмем Linear .
Отметьте подходящий вариант для вашего набора данных. В этом примере мы нажмем Linear . - Поскольку мы сравниваем пять различных продуктов во времени, Excel создает линию тренда для каждого отдельного продукта.Чтобы создать линейную линию тренда для продукта A, щелкните Product A и нажмите синюю кнопку OK .
- Теперь на диаграмме будет отображаться пунктирная линия тренда, представляющая линейную прогрессию продукта A. Обратите внимание, что Excel также добавил в легенду Linear (Product A) .
- Чтобы отобразить уравнение линии тренда на диаграмме, дважды щелкните линию тренда. В правой части экрана откроется окно Trendline Format .Установите флажок рядом с . Отобразите уравнение на графике в нижней части окна. Теперь уравнение появится на вашем графике.
Примечание. Вы можете создать отдельные линии тренда для любого количества переменных на диаграмме.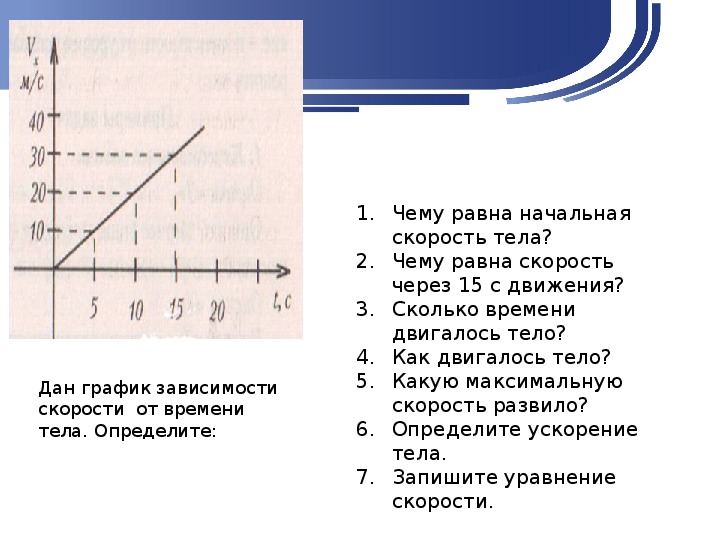 Например, вот наша диаграмма с линиями тренда для продукта A и продукта C.
Например, вот наша диаграмма с линиями тренда для продукта A и продукта C.
Чтобы добавить столбцы вверх/вниз: Столбики вверх/вниз недоступны для столбчатой диаграммы, но вы можете использовать их в линейной диаграмме, чтобы показать увеличение и уменьшение между точками данных.
Шаг 4. Настройка быстрого макета
- Второе раскрывающееся меню на панели инструментов — Quick Layout , которое позволяет вам быстро изменить расположение элементов на диаграмме (заголовки, условные обозначения, кластеры и т. д.).
- Имеется 11 вариантов быстрого макета. Наведите курсор на различные варианты объяснения и щелкните тот, который хотите применить.
Шаг 5. Изменение цвета
Следующее раскрывающееся меню на панели инструментов — Изменить цвета .Щелкните значок и выберите цветовую палитру, которая соответствует вашим потребностям (эти потребности могут быть эстетическими или соответствовать цветам и стилю вашего бренда).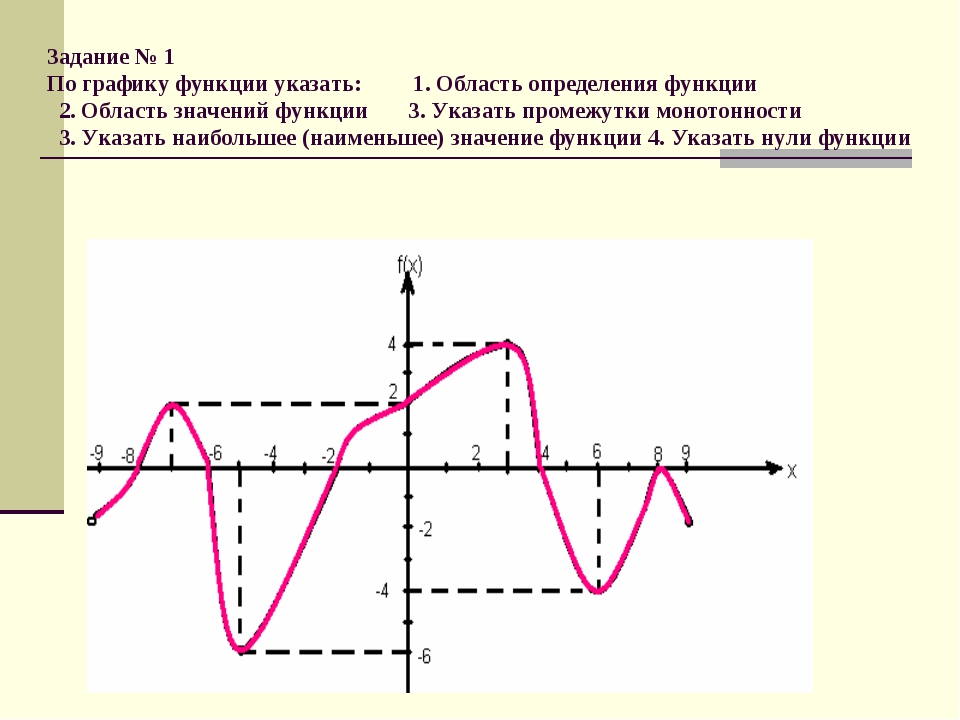
Шаг 6: Изменить стиль
Для кластерных гистограмм доступно 14 стилей диаграмм. Excel по умолчанию использует стиль 1, но вы можете выбрать любой из других стилей, чтобы изменить внешний вид диаграммы. Используйте стрелку справа от панели изображений, чтобы просмотреть другие параметры.
Шаг 7. Переключение строки/столбца
- Нажмите кнопку Switch Row/Column на панели инструментов, чтобы перевернуть оси.Примечание. Переворачивать оси для каждой диаграммы не всегда интуитивно понятно, например, если у вас более двух переменных.
В этом примере переключение строки и столбца меняет местами продукт и год (прибыль остается на оси Y). Диаграмма теперь сгруппирована по продуктам (не по годам), а легенда с цветовой кодировкой относится к году (а не к продукту). Чтобы избежать путаницы, нажмите на легенду и измените названия с Series на Years .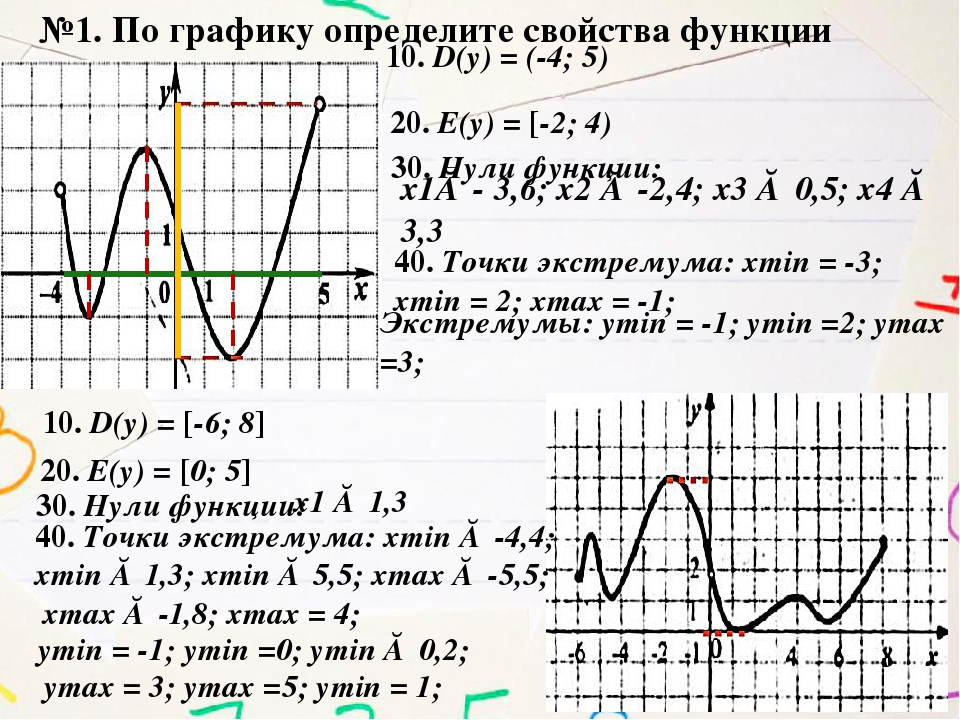
Шаг 8. Выберите данные
- Щелкните значок Select Data на панели инструментов, чтобы изменить диапазон ваших данных.
- Откроется окно. Введите нужный диапазон ячеек и нажмите кнопку OK . Диаграмма автоматически обновится, чтобы отразить этот новый диапазон данных.
Шаг 9: изменение типа диаграммы
- Щелкните раскрывающееся меню Изменить тип диаграммы .
- Здесь вы можете изменить тип диаграммы на любую из девяти категорий диаграмм, которые предлагает Excel. Конечно, убедитесь, что ваши данные подходят для выбранного вами типа диаграммы.
Вы также можете сохранить свою диаграмму как шаблон, нажав Сохранить как шаблон …
- Откроется диалоговое окно, в котором вы можете назвать свой шаблон. Excel автоматически создаст папку для ваших шаблонов для удобства организации. Нажмите синюю кнопку Сохранить .

Шаг 10. Перемещение диаграммы
- Щелкните значок Переместить диаграмму в крайнем правом углу панели инструментов.
- Появится диалоговое окно, в котором можно выбрать место для размещения диаграммы.Вы можете либо создать новый лист с этой диаграммой (Новый лист) , либо поместить эту диаграмму как объект на другой лист (Объект в) . Нажмите синюю кнопку OK .
Шаг 11. Изменение форматирования
- Вкладка Формат позволяет изменить форматирование всех элементов и текста на диаграмме, включая цвета, размер, форму, заливку и выравнивание, а также возможность вставки фигур. Перейдите на вкладку Формат и используйте доступные сочетания клавиш, чтобы создать диаграмму, отражающую бренд вашей организации (цвета, изображения и т. д.).).
- Щелкните раскрывающееся меню в верхней левой части панели инструментов и щелкните элемент диаграммы, который вы редактируете.

Шаг 12. Удаление диаграммы
Чтобы удалить диаграмму, просто щелкните ее и нажмите клавишу Удалить на клавиатуре.
Excel 2013: диаграммы
/en/excel2013/таблицы/контент/
Введение
Часто бывает сложно интерпретировать книги Excel, содержащие много данных. Диаграммы позволяют графически иллюстрировать данные рабочей книги, что упрощает визуализацию сравнений и трендов .
Необязательно: загрузите нашу рабочую тетрадь.
Понимание карт
Excel имеет несколько различных типов из диаграмм , что позволяет вам выбрать тот, который лучше всего соответствует вашим данным. Чтобы эффективно использовать диаграммы, вам необходимо понимать, как используются различные диаграммы.
Щелкните стрелки в слайд-шоу ниже, чтобы узнать больше о типах диаграмм в Excel.
В дополнение к типам диаграмм вам необходимо понять, как читать диаграмму . Диаграммы содержат несколько различных элементов или частей, которые могут помочь вам интерпретировать данные.
Нажмите кнопки в интерактивном ниже, чтобы узнать о различных частях диаграммы.
Легенда
Легенда указывает, какой ряд данных представляет каждый цвет на диаграмме.
В этом примере легенда идентифицирует разных продавцов на диаграмме.
Название диаграммы
Название должно четко описывать, что иллюстрирует диаграмма.
Вертикальная ось
Вертикальная ось (также известная как ось Y) — это вертикальная часть диаграммы.
Здесь вертикальная ось измеряет значение столбцов, поэтому ее также называют осью значений. В этом примере измеренным значением является чистый объем продаж каждого продавца.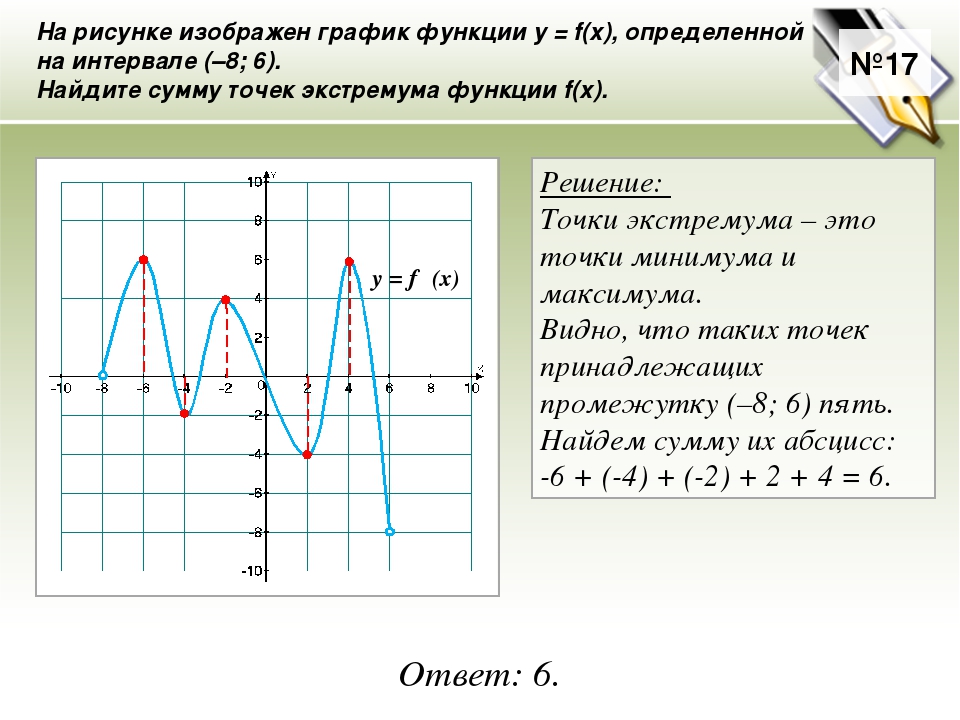
Горизонтальная ось
Горизонтальная ось (также известная как ось x) — это горизонтальная часть диаграммы.
Здесь горизонтальная ось определяет категорий на диаграмме. В этом примере каждый квартал продаж помещается в собственную группу .
Серия данных
Серия данных состоит из связанных точек данных на диаграмме.
В этом примере синие столбцы представляют чистые продажи Роберта Джонсона. Мы знаем, что его данные выделены синим цветом из-за легенды справа.
Читая ряд данных, мы видим, что Роберт был лучшим продавцом в 1 и 3 кварталах, а во 2 и 4 кварталах он был вторым по величине.
Чтобы вставить диаграмму:
- Выберите ячеек для построения диаграммы, включая заголовков столбцов и меток строк . Эти ячейки будут исходными данными для диаграммы. В нашем примере мы выберем ячейки A1:F6.
 Выбор ячеек A1:F6
Выбор ячеек A1:F6 - На вкладке Вставка щелкните нужную команду Диаграмма .В нашем примере мы выберем Столбец . Нажав команду Столбчатая диаграмма
- Выберите нужную диаграмму тип из раскрывающегося меню. Выбор типа диаграммы
- Выбранная диаграмма будет вставлена в рабочий лист .Вставленная диаграмма
Если вы не уверены, какой тип диаграммы использовать, команда Рекомендуемые диаграммы предложит несколько различных диаграмм на основе исходных данных.
Выбор команды «Рекомендуемые графики»
Макет и стиль диаграммы
После вставки диаграммы есть несколько вещей, которые вы можете изменить в способе отображения ваших данных.На вкладке Дизайн легко редактировать макет диаграммы и стиль .
- Excel позволяет добавлять элементов диаграммы — например, диаграмма заголовков , условных обозначений и данных меток — чтобы упростить чтение диаграммы.
 Чтобы добавить элемент диаграммы, щелкните команду Добавить элемент диаграммы на вкладке Дизайн , затем выберите нужный элемент из раскрывающегося меню.
Чтобы добавить элемент диаграммы, щелкните команду Добавить элемент диаграммы на вкладке Дизайн , затем выберите нужный элемент из раскрывающегося меню.Добавление заголовка диаграммы
- Чтобы отредактировать элемент диаграммы, например заголовок диаграммы , , просто дважды щелкните заполнитель и начните вводить текст. хотите добавить элементы диаграммы по отдельности, вы можете использовать один из предопределенных макетов Excel. Просто щелкните команду Quick Layout , затем выберите нужный макет из раскрывающегося меню. ощущение вашей диаграммы.Чтобы изменить стиль диаграммы, выберите нужный стиль из группы Стили диаграммы. и фильтруют данные диаграммы. Ярлыки форматирования диаграммы
Другие опции диаграммы
Существует множество других способов настройки и организации диаграмм.
 Например, Excel позволяет переупорядочивать данные диаграммы, изменять тип диаграммы и даже перемещать диаграмму в другое место в рабочей книге.
Например, Excel позволяет переупорядочивать данные диаграммы, изменять тип диаграммы и даже перемещать диаграмму в другое место в рабочей книге.Чтобы переключить данные строки и столбца:
Иногда вам может понадобиться изменить способ группировки ваших данных на диаграммах . Например, на приведенной ниже диаграмме данные о продажах книг сгруппированы по году со столбцами для в каждом жанре . Однако мы могли бы поменять местами строки и столбцы, чтобы на диаграмме данные были сгруппированы по жанру со столбцами для по каждому году . В обоих случаях диаграмма содержит одни и те же данные, просто они организованы по-разному.
Данные сгруппированы по годам со столбцами для каждого жанра 90 537- Выберите диаграмму , которую вы хотите изменить.
- На вкладке Design выберите команду Switch Row/Column .
 Щелкните команду Switch Rows/Columns
Щелкните команду Switch Rows/Columns - Строки и столбцы будут переключены . В нашем примере данные теперь сгруппированы по жанрам со столбцами для каждого года. Переключенные данные строки и столбца
Чтобы изменить тип диаграммы:
Если вы обнаружите, что ваши данные не подходят для определенной диаграммы, можно легко переключиться на новую диаграмму типа .В нашем примере мы изменим нашу диаграмму с диаграммы Column на диаграмму Line .
- На вкладке Design щелкните команду Change Chart Type . Щелкните команду Change Chart Type
- Появится диалоговое окно Change Chart Type . Выберите новую диаграмму типа и макет , затем нажмите OK . В нашем примере мы выберем диаграмму Line . Выбор нового типа диаграммы
- Появится выбранный тип диаграммы.
 В нашем примере линейная диаграмма упрощает просмотр тенденций в данных о продажах с течением времени. Новый тип диаграммы
В нашем примере линейная диаграмма упрощает просмотр тенденций в данных о продажах с течением времени. Новый тип диаграммы
Чтобы переместить диаграмму:
Всякий раз, когда вы вставляете новую диаграмму, она отображается как объект на том же рабочем листе, который содержит исходные данные. В качестве альтернативы вы можете переместить диаграмму на новый рабочий лист , чтобы упорядочить данные.
- Выберите диаграмму , которую вы хотите переместить.
- Щелкните вкладку Design , затем выберите команду Move Chart .Нажатие команды «Переместить диаграмму»
- Появится диалоговое окно «Переместить диаграмму ». Выберите желаемое местоположение для диаграммы. В нашем примере мы решим переместить его на Новый лист , который создаст новый рабочий лист.
- Щелкните OK .
 Перемещение диаграммы на новый рабочий лист
Перемещение диаграммы на новый рабочий лист - Диаграмма появится в выбранном месте. В нашем примере диаграмма теперь отображается на новом рабочем листе. Диаграмма на отдельном рабочем листе
Поддержание диаграмм в актуальном состоянии
По умолчанию при добавлении дополнительных данных в электронную таблицу диаграмма может не включать новые данные.Чтобы исправить это, вы можете настроить диапазон данных . Просто щелкните диаграмму, и она выделит диапазон данных в вашей электронной таблице. Затем вы можете щелкнуть и перетащить маркер в правом нижнем углу, чтобы изменить диапазон данных.
Если вы часто добавляете новые данные в электронную таблицу, обновление диапазона данных может стать утомительным. К счастью, есть более простой способ. Просто отформатируйте исходные данные как таблицу , затем создайте диаграмму на основе этой таблицы .Когда вы добавите дополнительные данные под таблицу, они будут автоматически включены как в таблицу, так и в диаграмму, что обеспечит согласованность и актуальность данных.

Посмотрите видео ниже, чтобы узнать, как использовать таблицы для обновления диаграмм.
Вызов!
- Откройте существующую книгу Excel . Если вы хотите, вы можете использовать нашу рабочую тетрадь.
- Используйте данные рабочего листа для создания диаграммы . Если вы используете пример, используйте диапазон ячеек A1:F6 в качестве исходных данных для диаграммы.
- Изменить макет диаграммы . Если вы используете пример, выберите Layout 8 .
- Применение стиля диаграммы .
- Переместить график. Если вы используете пример, переместите диаграмму на новый рабочий лист с именем Данные о продажах книг: 2008-2012 .

/en/excel2013/sparklines/content/
Как создать диаграмму или график в Excel [с видеоруководством]
Построение диаграмм и графиков — один из лучших способов визуализировать данные в ясной и понятной форме.(Чтобы узнать больше, ознакомьтесь с этим руководством по созданию лучших диаграмм.) Однако неудивительно, что некоторых людей немного пугает перспектива копаться в Microsoft Excel. (Правда, я обожаю Excel, но я работаю в отделе маркетинговых операций, так что это в значительной степени требование, чтобы мне нравился этот инструмент).
Я решил поделиться полезным видеоуроком, а также некоторыми пошаговыми инструкциями для тех, кто съеживается при мысли об организации электронной таблицы, полной данных, в диаграмму, которая на самом деле, как вы знаете, означает что-то .
Вот простые шаги, необходимые для построения диаграммы или графика в Excel.
Имейте в виду, что существует множество разных версий Excel, поэтому то, что вы видите на видео выше, может не всегда точно совпадать с тем, что вы увидите в своей версии.
 В видео я использовал Excel 2021 версии 16.49 для Max OS X.
В видео я использовал Excel 2021 версии 16.49 для Max OS X.Чтобы получить самые последние инструкции, я рекомендую вам следовать приведенным ниже письменным инструкциям (или загрузить их в формате PDF). Большинство кнопок и функций, которые вы увидите и прочитаете, очень похожи во всех версиях Excel.
Скачать демонстрационные данные | Инструкции по загрузке (Mac) | Скачать инструкцию (ПК)
Как построить график в Excel
- Введите данные в Excel.
- Выберите один из девяти вариантов графиков и диаграмм.
- Выделите свои данные и нажмите «Вставить» нужный график.
- При необходимости переключите данные на каждой оси.
- Настройте макет и цвета ваших данных.
- Измените размер условных обозначений диаграммы и меток осей.
- При необходимости измените параметры измерения по оси Y.

- При желании измените порядок данных.
- Назовите свой график.
- Экспортируйте свой график или диаграмму.
1. Введите данные в Excel.
Во-первых, вам нужно ввести данные в Excel. Возможно, вы экспортировали данные откуда-то еще, например, из маркетингового программного обеспечения или инструмента для проведения опросов.Или, может быть, вы вводите его вручную.
В приведенном ниже примере в столбце A у меня есть список ответов на вопрос «Показал ли входящий маркетинг рентабельность инвестиций?», а в столбцах B, C и D у меня есть ответы на вопрос: «Показывает ли ваш у компании есть официальное соглашение о продажах и маркетинге?» Например, столбец C, строка 2 показывает, что 49% людей, у которых есть SLA (соглашение об уровне обслуживания), также говорят, что входящий маркетинг продемонстрировал рентабельность инвестиций.
2. Выберите параметры графика и диаграммы.

В Excel ваши варианты диаграмм и графиков включают столбчатые (или гистограммы), линейные графики, круговые диаграммы, точечные диаграммы и многое другое. Посмотрите, как Excel определяет каждый из них на верхней панели навигации, как показано ниже:
.Чтобы найти параметры диаграммы и графика, выберите Вставить.
(Чтобы понять, какой тип диаграммы/графика лучше всего подходит для визуализации ваших данных, ознакомьтесь с нашей бесплатной электронной книгой «Как использовать визуализацию данных, чтобы привлечь внимание вашей аудитории».)
3.Выделите свои данные и вставьте нужный график в электронную таблицу.
В этом примере я буду использовать гистограмму для визуального представления данных. Чтобы сделать гистограмму, выделите данные и включите заголовки осей X и Y. Затем перейдите на вкладку «Вставка» и в разделе диаграмм щелкните значок столбца. Выберите нужный график в раскрывающемся окне.
В этом примере я выбрал первый вариант двухмерного столбца — просто потому, что я предпочитаю плоскую графику, а не трехмерный вид.
 См. полученную гистограмму ниже.
См. полученную гистограмму ниже.4. При необходимости переключите данные на каждой оси.
Если вы хотите переключить то, что отображается на осях X и Y, щелкните правой кнопкой мыши гистограмму, нажмите «Выбрать данные» и нажмите «Переключить строку/столбец». Это изменит порядок осей, которые несут какие фрагменты данных в списке, показанном ниже. Когда вы закончите, нажмите OK внизу.
Результирующий график будет выглядеть так:
5. Настройте макет и цвета данных.
Чтобы изменить макет маркировки и легенды, нажмите гистограмму, затем перейдите на вкладку «Дизайн диаграммы». Здесь вы можете выбрать, какой макет вы предпочитаете для заголовка диаграммы, названий осей и легенды. В моем примере, показанном ниже, я выбрал параметр, который отображал более мягкие цвета столбцов и легенды под диаграммой.
Для дальнейшего форматирования легенды щелкните ее, чтобы открыть боковую панель «Формат легенды», как показано ниже.
 Здесь вы можете изменить цвет заливки легенды, что, в свою очередь, изменит цвет самих столбцов.Чтобы отформатировать другие части диаграммы, щелкните их по отдельности, чтобы открыть соответствующее окно «Формат».
Здесь вы можете изменить цвет заливки легенды, что, в свою очередь, изменит цвет самих столбцов.Чтобы отформатировать другие части диаграммы, щелкните их по отдельности, чтобы открыть соответствующее окно «Формат».6. Измените размер условных обозначений диаграммы и меток осей.
Когда вы впервые создаете диаграмму в Excel, размер меток вашей оси и легенды может быть немного меньше, в зависимости от выбранного вами типа диаграммы или диаграммы (столбчатая, круговая, линейная и т. д.). диаграмме, вы захотите усилить эти метки, чтобы они были разборчивы.
Чтобы увеличить размер меток вашего графика, щелкните их по отдельности и вместо открытия нового окна «Формат» вернитесь на вкладку «Главная» в верхней панели навигации Excel.Затем используйте раскрывающиеся поля типа и размера шрифта, чтобы расширить или уменьшить легенду диаграммы и метки осей по своему вкусу.
7. При необходимости измените параметры измерения по оси Y.
Чтобы изменить тип измерения, отображаемый по оси Y, щелкните проценты по оси Y на диаграмме, чтобы открыть окно Формат оси.
 Здесь вы можете решить, хотите ли вы отображать единицы, расположенные на вкладке «Параметры оси», или хотите ли вы изменить, показывает ли ось Y проценты с 2 знаками после запятой или с 0 знаками после запятой.
Здесь вы можете решить, хотите ли вы отображать единицы, расположенные на вкладке «Параметры оси», или хотите ли вы изменить, показывает ли ось Y проценты с 2 знаками после запятой или с 0 знаками после запятой.Поскольку на моем графике максимальный процент оси Y автоматически устанавливается равным 60 %, я могу вручную изменить его на 100 %, чтобы представить мои данные в более универсальном масштабе. Для этого я могу выбрать параметр «Максимум» — два поля внизу в разделе «Границы» в окне «Формат оси» — и изменить значение с 0,6 на 1.
Результирующий график будет выглядеть так, как показано ниже (я увеличил размер шрифта по оси Y на вкладке «Главная», чтобы вы могли видеть разницу):
8.При желании измените порядок данных.
Чтобы отсортировать данные таким образом, чтобы ответы респондентов отображались в обратном порядке, щелкните правой кнопкой мыши график и щелкните Выбрать данные, чтобы открыть то же окно параметров, которое вы вызывали на шаге 3 выше.
 На этот раз щелкните стрелки вверх и вниз, как показано ниже, чтобы изменить порядок данных на диаграмме.
На этот раз щелкните стрелки вверх и вниз, как показано ниже, чтобы изменить порядок данных на диаграмме.Если у вас есть более двух строк данных для настройки, вы также можете переставить их в порядке возрастания или убывания. Для этого выделите все свои данные в ячейках над диаграммой, нажмите «Данные» и выберите «Сортировка», как показано ниже.Вы можете выбрать сортировку от меньшего к большему или от большего к меньшему, в зависимости от ваших предпочтений.
Результирующий график будет выглядеть так:
9. Назовите свой график.
Теперь самое интересное и простое: дать имя вашему графику. К настоящему моменту вы, возможно, уже поняли, как это сделать. Вот простой осветлитель.
Сразу после создания диаграммы заголовок, который появится, скорее всего, будет «Заголовок диаграммы» или что-то подобное, в зависимости от используемой версии Excel.Чтобы изменить эту метку, нажмите «Заголовок диаграммы», чтобы открыть курсор для ввода.
 Затем вы можете свободно настроить заголовок диаграммы.
Затем вы можете свободно настроить заголовок диаграммы.Если у вас есть заголовок, который вам нравится, нажмите «Главная» на верхней панели навигации и используйте параметры форматирования шрифта, чтобы придать заголовку то значение, которого он заслуживает. См. эти варианты и мой окончательный график ниже:
10. Экспортируйте график или диаграмму.
После того, как ваша диаграмма или график станут именно такими, как вы хотите, вы можете сохранить их как изображение, не делая скриншоты в электронной таблице.Этот метод даст вам чистое изображение диаграммы, которое можно вставить в презентацию PowerPoint, документ Canva или любой другой визуальный шаблон.
Чтобы сохранить график Excel в виде фотографии, щелкните правой кнопкой мыши график и выберите Сохранить как изображение… .
В диалоговом окне назовите фотографию вашего графика, выберите, где ее сохранить на своем компьютере, и выберите тип файла, в котором вы хотите ее сохранить.
 В этом примере я сохраняю его в формате JPEG в папку на рабочем столе.Наконец, нажмите Сохранить.
В этом примере я сохраняю его в формате JPEG в папку на рабочем столе.Наконец, нажмите Сохранить.У вас будет четкая фотография вашего графика или диаграммы, которую вы сможете добавить к любому визуальному дизайну.
Визуализируйте данные как профессионал
Это было довольно просто, правда? С помощью этого пошагового руководства вы сможете быстро создавать диаграммы и графики, визуализирующие самые сложные данные. Попробуйте использовать этот же учебник с различными типами графиков, такими как круговая диаграмма или линейный график, чтобы увидеть, какой формат лучше всего передает историю ваших данных. Вы даже можете попрактиковаться в настройке графиков и диаграмм с большим объемом данных, используя приведенные ниже бесплатные шаблоны Excel для маркетологов.
Примечание редактора: этот пост был первоначально опубликован в июне 2018 года и обновлен для полноты картины.
Как создать диаграмму от начала до конца
При написании отчета или статьи, разработке инфографики или презентации у вас может быть несколько цифр для включения.
 И хотя вы могли бы написать о них абзац, гораздо интереснее создать диаграмму, чтобы показать вашу информацию.
И хотя вы могли бы написать о них абзац, гораздо интереснее создать диаграмму, чтобы показать вашу информацию.Это связано с тем, что чтение чисел и попытка визуализировать их значение в уме — это совершенно иной опыт, чем просмотр диаграммы, визуализирующей их значение прямо перед вашими глазами.
Однако вы не хотите переусердствовать и начинать использовать диаграммы, когда это не имеет смысла или когда другой визуальный элемент — например, значки, иллюстрации или стоковые фотографии — может лучше передать вашу точку зрения.
Знать, когда создавать диаграмму, так же важно, как и знать, как это сделать, поэтому давайте сначала углубимся в этот вопрос.
Когда создавать диаграмму
Всегда будут случаи, когда у вас будут данные и статистика, которыми вы захотите поделиться, независимо от того, что вы создаете.Демонстрация этих данных на диаграмме дает вашей аудитории гораздо лучший способ понять ваши аргументы.
Вы можете использовать различные типы диаграмм, чтобы добавить визуальный элемент к своим словам и числам.
 Есть числовые диаграммы, а также организационные диаграммы, которые помогут вам визуализировать мысли и идеи.
Есть числовые диаграммы, а также организационные диаграммы, которые помогут вам визуализировать мысли и идеи.Если вы хотите предоставить визуальную помощь, чтобы помочь проиллюстрировать ваш контент, числовая или организационная диаграмма может быть оптимальным способом сделать это.
Хотя многие писатели и создатели контента склонны использовать стоковые фотографии в своем контенте, вместо них существует целый мир визуальных элементов.Попробуйте добавить одну из диаграмм, которые мы обсуждаем в этой статье, к вашему следующему контенту.
Вот пример включения контента в абзац, а не в диаграмму. Вы можете легко определить, какой из них является более полным сразу.
Как создать диаграмму
Мы разработали простой шестиэтапный процесс, который поможет вам определить, какой тип диаграммы лучше всего соответствует вашей информации, а затем создать диаграмму прямо в Visme для загрузки или встраивания в запись блога или на веб-страницу.

Шаг 1. Определите тип диаграммы
Во-первых, какой тип диаграммы лучше всего подходит для вашей информации?
У вас есть данные и статистика для ввода в числовую диаграмму или вы хотите использовать графический органайзер или организационную диаграмму для визуализации содержимого?
Числовые диаграммы
Существует несколько типов числовых диаграмм, которые можно создать прямо в Visme, просто начав с шаблона и введя данные в Graph Engine.
Visme также предлагает ряд диаграмм и виджетов данных за пределами Graph Engine, как вы можете видеть ниже.
Графический движок — это первая опция на вкладке данных Visme, которая открывает электронную таблицу и около 16 различных параметров диаграмм и графиков.
Давайте углубимся в каждый из типов числовых диаграмм, которые вы можете создать прямо в Graph Engine Visme.
Гистограммы
Столбчатая диаграмма может быть вертикальной или горизонтальной и используется для отображения различных частот или объемов данных в различных категориях.

Так, например, приведенный ниже шаблон гистограммы, доступный прямо в Visme, сравнивает крупнейшие компании в 2019 году на основе их доходов.
Вы также можете включать группы данных в гистограммы, как в этом шаблоне ниже.
Обратите внимание на то, что внизу есть четыре разные категории, каждая с тремя разными фрагментами данных.
Гистограммы, как правило, чрезвычайно универсальны и могут помочь визуализировать все виды данных и информации, чтобы помочь вам сразу увидеть, какие переменные имеют самые высокие значения или частоты, а какие — самые низкие.
Линейные графики
Линейная диаграмма — это еще одна распространенная визуализация данных, которая позволяет вам демонстрировать изменения значения за набор определенных интервалов, обычно сегментов времени.
В приведенном ниже шаблоне линейной диаграммы показана динамика трех различных продуктов по месяцам.
Линейную диаграмму также можно использовать для демонстрации данных о тенденциях, таких как количество запросов по определенному ключевому слову или модному слову в Google и других поисковых системах.
Линейные диаграммы
лучше всего использовать для демонстрации тенденций, как правило, с течением времени, хотя они не должны ограничиваться такими данными.
Попробуйте линейную диаграмму в следующий раз, когда будете пытаться определить, имеет ли что-то положительную или отрицательную тенденцию, чтобы вы и ваша аудитория могли определить это, просто взглянув на диаграмму.
Круговые диаграммы
Круговая диаграмма используется для отображения частей целого, чаще всего при отображении процентов, так как они всегда будут частями 100%.
Один из лучших способов продемонстрировать, как следует использовать круговую диаграмму, — это шаблон ниже, в котором показано, как владельцы смартфонов проводят время со своими телефонами в течение дня.
Круговые диаграммытакже отлично подходят для представления демографической информации.
Если вы пытаетесь изобразить части целого или визуализировать различные проценты, круговая диаграмма будет идеальным типом диаграммы для вас.

Радиолокационные карты
Радарная диаграмма, также известная как паутинная диаграмма, веб-диаграмма или полярная диаграмма, является хорошим методом визуального сравнения различных вещей в одной и той же категории, таких как функции на разных смартфонах, вкусы разных сортов пива или области выступления гимнастки.
Взгляните на этот пример, сравнивающий разные вкусы двух разных сортов пива.
Радарная диаграмма также может быть отличным способом визуализации результатов, например, в программе гимнастки или производительности сотрудника во время его ежегодного обзора.
Вы можете включить только одну переменную, чтобы продемонстрировать одного сотрудника или один бренд, или вы можете сравнить, включив несколько переменных.
Вы можете включить контур только ваших точек или использовать полупрозрачный цвет, чтобы сделать сравнение более очевидным.Вы не хотите использовать непрозрачные цвета, которые закрывают другие переменные на вашей диаграмме.

Пиктограммы
Пиктограмма или массив — это скорее визуальное представление чисел, чем точная диаграмма, но они идеально подходят для демонстрации чисел.
Пиктограммы, как правило, используют значки или графику вместо чисел, чтобы с первого взгляда дать представление о том, сколько людей, вещей и т. д. содержится в наборе данных.
Взгляните на этот пример пиктограммы, которая подчеркивает уровень счастья сотрудников, используя различные типы смайликов в качестве значков.
Хотя этот пример включает один значок для каждого процента, вы также можете добавить ключ или легенду, чтобы зрители знали, что один значок равен 10 или около того людям или процентным пунктам.
Еще один отличный пример — демонстрация использования эмодзи среди мужчин и женщин, как в примере ниже.
Существует так много разных способов использования пиктограмм, когда вы пытаетесь визуализировать числа на графике. Пиктограммы — это распространенный тип визуализации, который можно увидеть внутри инфографики.

Организационные схемы
Не каждая созданная вами диаграмма будет числовой диаграммой.Есть так много причин организовать ваш контент, чтобы его было еще легче усваивать.
Давайте рассмотрим несколько распространенных типов организационных диаграмм и графических органайзеров, которые помогут вам еще яснее продемонстрировать свои идеи.
Блок-схемы
Блок-схема — это организационная диаграмма, которая проводит зрителя через процессы, шаги и многое другое, и они невероятно универсальны.
Фактически, вы можете создавать собственные блок-схемы прямо в Visme с любыми типами линий, пузырьков и шрифтов, которые вы выберете.
Вы можете создавать блок-схемы для личных процессов, как в приведенном ниже примере, доступном в виде настраиваемого шаблона.
Вы также можете создать блок-схему, которая поможет вам определить, пора ли сделать следующий шаг в вашем бизнесе, например изменить дизайн вашего веб-сайта.
Это отличный способ упорядочить различные шаги, процессы или создать диаграмму «да/нет», чтобы поделиться ею с вашим контентом.

Сравнительные таблицы
Сравнительная таблица — это идеальный способ визуально сравнить две или более вещи, будь то продукт, характеристика, компания или другое сравнение.
Возьмите этот пример таблицы сравнения фруктов и овощей и как их классифицировать.
Другой пример использования сравнительной таблицы для взвешивания плюсов и минусов, например, путешествия в одиночку или в паре. Этот шаблон сравнительной диаграммы ниже доступен для настройки в Visme.
Эти типы диаграмм идеально подходят для демонстрации параллельных сравнений двух или более элементов и могут быть очень привлекательными визуально.
Иерархические диаграммы
Иерархические диаграммы — это тип организационной диаграммы, которая показывает, как все происходит сверху вниз.Есть несколько разных способов визуализировать это, будь то блок-схема, воронкообразная диаграмма, пирамидальная диаграмма и многое другое.
У нас есть несколько различных типов диаграмм иерархии, доступных в Visme, от визуализации иерархии команды до демонстрации воронки продаж.

Это отличный пример того, как иерархическая диаграмма может работать для демонстрации команды над проектом или в отделе компании, чтобы все знали, кто за кого отвечает.
Но иерархические диаграммы можно использовать и для большего, как в приведенном ниже примере шаблона, который охватывает иерархию потребностей SEO от наиболее важных до наименее важных.
Организуйте понятия сверху вниз, от меньшего к большему и от наиболее важного к наименее важному с помощью иерархической диаграммы.
Диаграммы Венна
Диаграмма Венна — это еще один способ сравнить и противопоставить различные концепции и идеи. На вашей диаграмме Венна может быть два разных круга, три, четыре и даже больше.
Давайте рассмотрим несколько различных примеров диаграмм Венна, которые вы можете редактировать и настраивать прямо в Visme.
Приведенный ниже шаблон представляет собой базовую диаграмму Венна с двумя кругами, которая позволяет сравнивать и противопоставлять две идеи.

В приведенный выше шаблон можно вставлять любые идеи, например молоко или сок, рекламу или маркетинг и многое другое.
Приведенная ниже диаграмма Венна помогает упорядочить еще более сложные идеи, например, что смешивать с кофе для приготовления разных напитков.
Существует так много разных способов создания и настройки диаграмм Венна, которые помогают сравнивать, противопоставлять и комбинировать идеи.
Как только вы поймете, какие типы диаграмм доступны вам и как ваши данные или информация могут в них вписаться, вам будет легче определить тип диаграммы.Выбрав числовую или организационную диаграмму, вы можете перейти ко второму шагу.
Шаг 2. Начните с шаблона
Как я уже упоминал в этой статье, у нас есть множество различных настраиваемых шаблонов, доступных в Visme, чтобы вы могли создавать и редактировать свои диаграммы.
Вы можете просмотреть выбор шаблонов диаграмм Visme, чтобы найти вариант, который выглядит так, как будто он легко соответствует вашей информации.

Использование шаблона может помочь подготовить основу вашего проекта еще до того, как вы приступите к дизайну, что значительно сократит время проекта.
Каждый из шаблонов Visme полностью настраивается, что означает, что вы можете найти тот, который имеет необходимые элементы диаграммы, а затем добавить свои собственные данные, изменить цвета и шрифты, добавить различные значки и фотографии и многое другое!
Шаг 3. Соберите информацию
После того, как вы выбрали шаблон и оказались в редакторе Visme, пришло время собрать информацию для включения в ваш новый дизайн.
Независимо от того, используете ли вы числовую диаграмму для демонстрации данных и статистики или графическую организаторскую диаграмму для визуализации слов и информации, наличие всего необходимого для ввода в одном месте может сделать вашу жизнь намного проще.
Шаг 4. Вставьте свои данные
Ваш следующий шаг — добавить данные или содержимое прямо в дизайн! С Visme это очень просто.

Если вы создаете числовую диаграмму, просто подключите свои данные к Graph Engine и посмотрите, как они выстроятся на вашей диаграмме.
А если вместо этого вы работаете с организационной диаграммой, такой как блок-схема или диаграмма Венна, просто используйте текстовый редактор, чтобы добавить свой контент и перетащите его туда, где вы хотите, чтобы он находился в графическом органайзере.
Шаг 5. Создайте свою диаграмму
Теперь, если есть трудная часть, когда дело доходит до создания диаграммы, это самая сложная часть. Но только потому, что есть определенные правила, которых нужно придерживаться при создании визуально привлекательного дизайна.
Кроме того, при создании диаграммы в Visme у вас есть выбор из множества различных элементов дизайна, но нам нравится думать, что это хорошая проблема.
Давайте рассмотрим несколько основных правил построения диаграмм.
1.Добавляйте в круговую диаграмму не более 7 фрагментов данных.

Круговые диаграммы отлично подходят для представления частей целого, но они не подходят для наглядных представлений о конкретных числах. Вот почему вы хотите, чтобы ваши части целого были минимальными, включая не более 7 различных переменных в одной круговой диаграмме.
Взгляните, как небольшое количество фрагментов данных упрощает просмотр процентов на этой круговой диаграмме.
Включение слишком большого количества переменных приводит к тому, что каждый кусок пирога становится все меньше и меньше, пока вы не будете уверены, какой кусок стоит больше, чем следующий.
2. Упорядочить данные для более организованной диаграммы.
Когда дело доходит до разработки гистограммы, вы можете расположить данные повсюду, причем самые высокие столбцы будут торчать в разные стороны.
Или вы можете создать целостную и организованную диаграмму, разместив данные в порядке убывания слева направо, как в примере ниже.
Имейте в виду, что не все типы диаграмм могут быть организованы таким образом.
 Если вы создаете диаграмму для определения частоты или корреляции, например, в случае гистограммы или точечной диаграммы, ваши результаты зависят от того, где они находятся на каждой оси.
Если вы создаете диаграмму для определения частоты или корреляции, например, в случае гистограммы или точечной диаграммы, ваши результаты зависят от того, где они находятся на каждой оси.Но в случае гистограммы или круговой диаграммы, где порядок фрагментов данных не имеет значения, обязательно организуйте их, чтобы улучшить общий вид вашего дизайна.
3. Придерживайтесь плоского дизайна, а не трехмерного.
Несмотря на то, что дизайн 3D-диаграммы может создать классный эффект и в некоторых случаях полезен, чаще всего он фактически искажает внешний вид ваших данных.
Это чаще всего встречается в трехмерных круговых диаграммах, когда из-за угла и размера диаграммы некоторые части круговой диаграммы могут казаться больше, чем они есть на самом деле.
Как я уже сказал, в некоторых случаях дизайн 3D-диаграмм имеет смысл, поэтому мы предоставляем всем пользователям Visme свободу самим определять, какая версия им нужна.
Тем не менее, в современном дизайне рекомендуется всегда использовать плоский дизайн, а не 3D, независимо от того, что вы создаете.

4. Используйте легенду только при необходимости.
Легенда или ключ позволяют пользователям узнать, какие фрагменты данных отображаются на диаграмме. Однако часть этой информации может быть очевидна из названия диаграммы и других элементов, что делает необходимость в легенде устаревшей.
Взгляните, например, на эту линейную диаграмму. Поскольку есть только одна переменная, которую мы отслеживаем, включая легенду, чтобы зрители знали, что означает линия, это было бы излишним и только загромождало бы ваш дизайн.
Используйте легенду в дизайне диаграммы только в случае необходимости, чтобы различать разные переменные. Вы можете легко включать и выключать это в Graph Engine Visme.
5. Отключите представление сетки.
Представление сетки на диаграмме сохраняет линии для каждой точки на каждой оси и может упростить более точное отображение измерений на диаграмме.
Взгляните на этот пример ниже с включенным видом сетки.
Хотя представление сетки полезно в тех случаях, когда гистограммы или точки данных расположены близко друг к другу, и вам нужна небольшая помощь, чтобы визуализировать их различия, они могут загромождать дизайн более очевидными скачками значений.

Как правило, выключайте представление сетки в каждом дизайне диаграмм, за исключением случаев, когда это абсолютно необходимо для правильного чтения данных.
6. Используйте контрастные цвета для каждого ряда данных.
Не позволяйте вашим линиям или столбцам смешиваться друг с другом, создавая нечеткую и скучную диаграмму.Это особенно важно в линейных диаграммах, когда вам нужно четко отличать каждую переменную от других.
Эти три линии окрашены в разные яркие цвета, что позволяет каждой из них выделяться и позволяет зрителю четко находить точки данных каждой переменной.
Если вы хотите выделить конкретное значение, чтобы привлечь к этой переменной еще больше внимания, чем к остальным, вы также можете выделить одну переменную контрастным цветом, чтобы ваша аудитория уделяла ей больше внимания.
Просто убедитесь, что при цветовом кодировании переменных вы всегда используете контрастные цвета, которые позволяют им выделяться друг против друга.

7. Включите цвета вашего бренда.
Еще один отличный способ раскрасить вашу диаграмму — включить цвета вашего бренда. Вы можете легко добавить их в свою диаграмму, если вы собрали свой бренд-кит в Visme.
Просто введите шестнадцатеричные коды цветов вашего бренда, загрузите шрифты вашего бренда и приготовьтесь к полной маркировке каждого из ваших творений всего за пару кликов.
Фирменные цвета и шрифты отображаются в верхней части меню выбора цветов и шрифтов, что упрощает поиск и выбор фирменных вариантов.
8. Используйте один шрифт, но два веса.
Спаривание шрифтов — это отдельное искусство. Сделайте свою жизнь проще и придерживайтесь одного шрифта, но двух разных начертаний в дизайне диаграммы.
Используйте шрифт, выделенный полужирным шрифтом, в заголовке диаграммы и метках осей, а обычный или облегченный вариант — в условных обозначениях и метках данных. В организационной диаграмме используйте полужирный шрифт для заголовков и подзаголовков и обычный или светлый шрифт для основного содержания.

Это помогает создать минималистичный, чистый вид вокруг вашей диаграммы, чтобы ваши данные были в центре внимания.В конце концов, весь смысл вашей диаграммы состоит в том, чтобы показать визуальную информацию.
9. Играйте с размерами диаграмм.
В Visme вы можете легко перетаскивать угол диаграммы, чтобы сделать ее больше, меньше, тоньше, толще и т. д.
Играя с этим, обратите внимание на то, как выглядят ваши данные. По мере увеличения ширины диаграммы ваши данные будут распространяться дальше, а по мере уменьшения ширины диаграммы ваши данные будут располагаться ближе друг к другу.
Если вы создаете диаграмму во всю ширину вашего дизайна, будь то отчет, инфографика, презентация или другой тип контента, и вы замечаете, что трудно отличить тенденции или точки данных, попробуйте поиграть с размером.
Сделайте диаграмму на половину или три четверти ширины страницы, чтобы увидеть, сделает ли это различия в ваших данных более очевидными.

Поскольку точки вашей оси будут изменяться по мере изменения размера диаграммы, это не повлияет на ваши данные.Это может просто облегчить чтение.
10. Добавьте элементы дизайна, представляющие вашу информацию.
Вам не нужно полностью доверять дизайн своей диаграммы. Добавьте различную графику, значки, фотографии и многое другое, что может рассказать еще более увлекательную историю.
Например, если вы создаете круговую диаграмму о том, как группа людей пьет кофе, поместите диаграмму в кофейную чашку.
Если вы создаете сравнительную диаграмму, в которой сравниваете различные продукты или функции, включите значки, которые помогут визуально представить, что представляют собой эти продукты и функции, как в примере шаблона ниже.
Или рассмотрите возможность использования значков для легенды или ключа вместо текста, чтобы добавить дополнительный уровень дизайна к вашему фрагменту контента.
11. Добавить анимацию и интерактивность.

Не позволяйте диаграмме просто сидеть и превращаться в застойную часть визуализации данных. С Visme вам предоставляются всевозможные варианты анимации и интерактивности, которые помогут воплотить вашу информацию в жизнь.
Если вы встроите свои диаграммы на веб-страницу или отправите ссылку на живой Visme своим коллегам или клиентам, ваш зритель сможет увидеть, как каждый отдельный фрагмент данных в вашей диаграмме оживает в одном из наших вариантов автоматической анимации.
Живая диаграмма также позволяет добавлять интерактивные параметры, например, дать пользователю возможность навести курсор на каждую точку данных, чтобы увидеть ее точное значение.
Разрешение вашему пользователю взаимодействовать с данными в вашей диаграмме создает совершенно новое измерение, которое вы не можете воспроизвести с другими создателями диаграмм.
Шаг 6. Поделитесь своей диаграммой
Теперь, когда вы завершили свой дизайн и добавили анимацию, чтобы по-настоящему заинтересовать вашу аудиторию, пришло время для последнего шага — фактического размещения вашей диаграммы перед вашим зрителем.

С Visme у вас есть три различных варианта обмена картами.
Вы можете загрузить его в одном из пяти различных форматов, включая JPG, PNG, PDF, PPT и HTML5. Последние два дают вам возможность делиться диаграммами в автономном режиме в презентациях и других типах контента.
Вы можете создать общедоступную или частную ссылку для общего доступа, которая открывает живой Visme со всей вашей анимацией и интерактивностью, доступной прямо в вашем творении.
Если вы решите опубликовать его и создать общедоступную ссылку, вы также получите доступ ко всем видам аналитики для отслеживания его эффективности.
Или вы можете получить HTML-код для встраивания, чтобы вставить его прямо в статью блога или веб-страницу, которая будет встраивать интерактивную диаграмму прямо на ваш веб-сайт, чтобы ваши зрители могли поиграть с ней.
Создание диаграммы с помощью Visme
Готовы создать собственную диаграмму прямо в Visme? Попробуйте Graph Engine и начните визуализировать свои данные и информацию с помощью собственной диаграммы.

Начните работу с шаблона, введите свою информацию и погрузитесь в свой дизайн. Поделитесь с нами всеми своими творениями в социальных сетях, пометив #MyVisme!
основных типов диаграмм для визуализации данных
Диаграммы являются важной частью работы с данными, поскольку они позволяют сжать большие объемы данных в удобном для понимания формате.Визуализация данных может дать понимание тем, кто впервые смотрит на данные, а также передать результаты другим, которые не будут видеть необработанные данные. Существует бесчисленное множество типов диаграмм, каждый из которых имеет разные варианты использования. Часто самой сложной частью создания визуализации данных является определение того, какой тип диаграммы лучше всего подходит для поставленной задачи.
Выбор типа диаграммы зависит от множества факторов. Какие типы показателей, функций или других переменных вы планируете отображать? Кто является аудиторией, перед которой вы планируете выступать — это просто первоначальное исследование для себя или вы представляете более широкую аудиторию? Какой вывод вы хотите, чтобы сделал читатель?
В этой статье мы предоставим обзор основных типов диаграмм, которые чаще всего предлагаются инструментами визуализации.
 С этими диаграммами у вас будет широкий набор инструментов для удовлетворения ваших потребностей в визуализации данных. Рекомендации о том, когда выбирать каждый из них в зависимости от варианта использования, описаны в следующей статье.
С этими диаграммами у вас будет широкий набор инструментов для удовлетворения ваших потребностей в визуализации данных. Рекомендации о том, когда выбирать каждый из них в зависимости от варианта использования, описаны в следующей статье.Основополагающая четверка
В своей книге «Покажи мне числа» Стивен Фью предлагает четыре основных способа кодирования числовых значений, указывающих позиционное значение с помощью полос, линий, точек и прямоугольников. Итак, мы начнем с четырех основных типов диаграмм, по одной для каждого из этих средств кодирования значений.
Гистограмма
На гистограмме значения обозначаются длиной столбцов, каждый из которых соответствует измеряемой группе.Гистограммы могут быть ориентированы вертикально или горизонтально; вертикальные гистограммы иногда называют столбчатыми диаграммами. Горизонтальные гистограммы — хороший вариант, когда нужно построить много столбцов или метки на них требуют дополнительного места, чтобы их можно было прочитать.

Линейный график
Линейные диаграммы показывают изменения значений при непрерывных измерениях, например, с течением времени. Движение линии вверх или вниз помогает выявить положительные и отрицательные изменения соответственно. Он также может выявить общие тенденции, чтобы помочь читателю сделать прогнозы или прогнозы будущих результатов.Несколько линейных диаграмм также могут привести к другим связанным диаграммам, таким как спарклайн или график хребта.
Диаграмма рассеяния
Точечная диаграмма отображает значения двух числовых переменных с помощью точек, расположенных на двух осях: по одной для каждой переменной. Диаграммы рассеяния — это универсальная демонстрация взаимосвязи между нанесенными на график переменными — независимо от того, является ли эта корреляция сильной или слабой, положительной или отрицательной, линейной или нелинейной. Диаграммы рассеяния также отлично подходят для выявления точек выбросов и возможных пробелов в данных.

Коробчатая диаграмма
Ящичная диаграмма использует блоки и усы для суммирования распределения значений в измеренных группах. Положения прямоугольника и концов усов показывают области, в которых находится большая часть данных. Чаще всего мы видим коробчатые диаграммы, когда у нас есть несколько групп для сравнения друг с другом; другие диаграммы с большей детализацией предпочтительнее, когда у нас есть только одна группа для построения.
Таблицы и отдельные значения
Прежде чем перейти к другим типам диаграмм, стоит уделить немного времени тому, чтобы оценить возможность отображения только необработанных чисел.В частности, когда у вас есть только одно число для отображения, простое отображение значения является разумным подходом к отображению данных. Когда точные значения представляют интерес для анализа, вы можете включить их в сопроводительную таблицу или с помощью аннотаций к графической визуализации.
Общие варианты
Дополнительные типы диаграмм могут появиться в результате изменения способов использования кодировок или включения дополнительных кодировок.
 Вторичные кодировки, такие как площадь, форма и цвет, могут быть полезны для добавления дополнительных переменных к более простым типам диаграмм.
Вторичные кодировки, такие как площадь, форма и цвет, могут быть полезны для добавления дополнительных переменных к более простым типам диаграмм.Гистограмма
Если группы, изображенные на гистограмме, на самом деле являются непрерывными числовыми диапазонами, мы можем соединить столбцы вместе, чтобы создать гистограмму. Длина столбцов на гистограммах обычно соответствует количеству точек данных, а их шаблоны демонстрируют распределение переменных в ваших данных. Другой тип диаграммы, такой как линейная диаграмма, обычно используется, когда значение по вертикали не является подсчетом частоты.
Столбчатая диаграмма с накоплением
Одной из модификаций стандартной гистограммы является разделение каждого столбца на несколько меньших столбцов на основе значений второй группирующей переменной, называемой гистограммой с накоплением.Это позволяет не только сравнивать значения основных групп, как на обычной гистограмме, но и иллюстрировать относительную разбивку каждой группы в целом на составные части.

Сгруппированная гистограмма
Если бы, с другой стороны, вложенные столбцы были помещены рядом друг с другом в кластеры, а не в стопки, мы получили бы сгруппированную гистограмму. Сгруппированная столбчатая диаграмма не позволяет сравнивать итоги по основным группам, но гораздо лучше позволяет сравнивать подгруппы.
Точечный график
Точечный график похож на столбчатую диаграмму в том смысле, что он показывает значения для различных категориальных группировок, но кодирует значения на основе положения точки, а не длины столбца. Точечные диаграммы полезны, когда вам нужно сравнить категории, но нулевой базовый уровень не информативен и не полезен. Вы также можете думать о точечном графике как о линейном графике с удаленной линией, чтобы его можно было использовать с переменными с неупорядоченными категориями, а не только с непрерывными или упорядоченными переменными.
Диаграмма с областями
Диаграмма с областями начинается с той же основы, что и линейная диаграмма — точки значений, соединенные линейными сегментами, — но добавляет концепцию гистограммы с затенением между линией и базовой линией.
 Эту диаграмму чаще всего можно увидеть в сочетании с концепцией суммирования, чтобы показать, как сумма изменилась с течением времени, а также как изменились вклады ее компонентов.
Эту диаграмму чаще всего можно увидеть в сочетании с концепцией суммирования, чтобы показать, как сумма изменилась с течением времени, а также как изменились вклады ее компонентов.Двухосная диаграмма
Диаграммы с двумя осями накладываются на две разные диаграммы с общей горизонтальной осью, но с потенциально разными масштабами вертикальной оси (по одной для каждой диаграммы компонентов).Это может быть полезно, чтобы показать прямое сравнение между двумя наборами вертикальных значений, а также включить контекст переменной горизонтальной оси. Обычно используются разные типы базовых диаграмм, такие как комбинация столбцов и линий, чтобы избежать путаницы с различными шкалами осей для каждой компонентной диаграммы.
Пузырьковая диаграмма
Другой способ показать взаимосвязь между тремя переменными — модифицировать точечный график. Когда третья переменная является категориальной, точки могут использовать разные формы или цвета для обозначения принадлежности к группе.
 Если точки данных каким-то образом упорядочены, точки также можно соединить с отрезками, чтобы показать последовательность значений. Когда третья переменная является числовой по своей природе, именно здесь появляется пузырьковая диаграмма. Пузырьковая диаграмма строится на основе диаграммы рассеяния, когда значение третьей переменной определяет размер каждой точки.
Если точки данных каким-то образом упорядочены, точки также можно соединить с отрезками, чтобы показать последовательность значений. Когда третья переменная является числовой по своей природе, именно здесь появляется пузырьковая диаграмма. Пузырьковая диаграмма строится на основе диаграммы рассеяния, когда значение третьей переменной определяет размер каждой точки.Кривая плотности
Кривая плотности или оценка плотности ядра — это альтернативный способ отображения распределения данных вместо гистограммы.Вместо того, чтобы собирать точки данных в ячейки частот, каждая точка данных вносит небольшой объем данных, совокупность которых становится кривой плотности. Хотя кривые плотности могут подразумевать некоторые значения данных, которые не существуют, они могут быть хорошим способом сгладить шум в данных, чтобы получить представление о сигнале распределения.
Сюжет для скрипки
Альтернативой ящичковому подходу к сравнению распределения значений между группами является скрипичный график.
 На скрипичном графике каждый набор прямоугольников и усов заменяется кривой плотности, построенной вокруг центральной базовой линии.Это может обеспечить лучшее сравнение форм данных между группами, хотя и теряется при сравнении точных статистических значений. Частой вариацией для скрипичных сюжетов является добавление маркировки в виде прямоугольника поверх скрипичного сюжета, чтобы получить лучшее из обоих миров.
На скрипичном графике каждый набор прямоугольников и усов заменяется кривой плотности, построенной вокруг центральной базовой линии.Это может обеспечить лучшее сравнение форм данных между группами, хотя и теряется при сравнении точных статистических значений. Частой вариацией для скрипичных сюжетов является добавление маркировки в виде прямоугольника поверх скрипичного сюжета, чтобы получить лучшее из обоих миров.Тепловая карта
Тепловая карта представляет собой сетку значений на основе двух представляющих интерес переменных. Переменные оси могут быть числовыми или категориальными; сетка создается путем деления каждой переменной на диапазоны или уровни, как гистограмма или гистограмма.Ячейки сетки окрашиваются в зависимости от значения, часто более темные цвета соответствуют более высоким значениям. Тепловая карта может быть интересной альтернативой точечной диаграмме, когда нужно построить много точек данных, но плотность точек затрудняет просмотр истинной взаимосвязи между переменными.

Карты специалиста
Существует множество дополнительных диаграмм, которые кодируют данные другими способами для конкретных случаев использования. Xenographics включает в себя коллекцию некоторых причудливых диаграмм, которые были созданы для очень конкретных целей.Тем не менее, у некоторых из этих диаграмм есть случаи использования, которые достаточно распространены, чтобы их можно было считать необходимым знать.
Круговая диаграмма
Вы можете быть удивлены, увидев, что круговые диаграммы изолированы здесь, в разделе «Специалист», учитывая, насколько часто они используются. Однако в круговых диаграммах используется необычная кодировка, изображающая значения в виде областей, вырезанных из круглой формы. Поскольку круговая диаграмма обычно не имеет маркировки значений по периметру, обычно трудно получить четкое представление о точных размерах секторов.Тем не менее, круговая диаграмма и ее двоюродный брат кольцевая диаграмма преуспели в том, чтобы сообщить читателю, что сравнение частей с целым должно быть основным выводом из визуализации.

Воронкообразная диаграмма
Воронкообразная диаграмма часто используется в бизнес-контекстах, где необходимо отслеживать посетителей или пользователей в конвейерном потоке. На диаграмме показано, сколько пользователей доходит до каждого этапа отслеживаемого процесса, исходя из ширины воронки на каждом этапе разделения. Сужение воронки помогает продать аналогию, но может запутать истинные коэффициенты конверсии.Гистограмма часто может выполнять ту же задачу, что и воронкообразная диаграмма, но с более четким представлением данных.
Пулевая диаграмма
Маркированная диаграмма дополняет один столбец дополнительными метками, указывающими, как контекстуализировать значение этого столбца. Обычно это означает перпендикулярную линию, показывающую целевое значение, а также затенение фона для обеспечения дополнительных показателей производительности. Пулевые диаграммы обычно используются для нескольких показателей и более компактны для отображения, чем другие типы более причудливых датчиков.

Графики на основе карты
Существует несколько семейств специальных графиков, сгруппированных по использованию, но мы завершим эту статью, коснувшись одного из них: картографических или геопространственных графиков. Когда значения в наборе данных соответствуют фактическим географическим местоположениям, может быть полезно нанести их на какую-либо карту. Распространенным примером такого типа карты является картограмма, подобная приведенной выше. При этом используется подход тепловой карты к изображению значения с помощью цвета, но вместо того, чтобы отображать значения в сетке, они заполняются областями на карте.
Чтобы получить удобное справочное руководство по другим типам диаграмм и тому, когда их следует использовать, ознакомьтесь с нашей бесплатной электронной книгой «Как выбрать правильную визуализацию данных».
Как создать диаграмму даты или времени в Excel
Если у вас есть данные, включающие информацию о времени, вам могут понадобиться некоторые специальные приемы, чтобы заставить Excel помочь вам создавать полезные диаграммы.
 Вот несколько советов по редактированию данных о времени и дате в диаграмме Excel. Эти функции применимы к Excel 2007–2013, хотя конкретные шаги зависят от вашей версии.Изображения были сделаны с использованием Excel 2013 в ОС Windows 7.
Вот несколько советов по редактированию данных о времени и дате в диаграмме Excel. Эти функции применимы к Excel 2007–2013, хотя конкретные шаги зависят от вашей версии.Изображения были сделаны с использованием Excel 2013 в ОС Windows 7.Используйте XY — точечную диаграмму
Безусловно, самый простой способ отображения временных данных — это использование точечной диаграммы. Точечные диаграммы автоматически берут данные о дате или времени и превращают их в ось шкалы времени. Когда вы выбираете диапазон дат или времени и данные, связанные с ним, Excel делает все возможное для организации информации в диаграмме со шкалой времени на оси X.
Однако лучшее предположение Excel может оказаться не таким полезным, как вам нужно.В этом примере мы хотим увидеть, как время суток влияет на наши рядовые данные. Полученная точечная диаграмма хорошо отображает ряд данных, но временная шкала по умолчанию представляет собой случайные единицы времени.
Чтобы использовать наш пример, загрузите временную диаграмму Excel
Чтобы настроить отображение шкалы времени по оси X:
- Щелкните диаграмму, чтобы открыть область области диаграммы .

- Нажмите Параметры диаграммы и выберите Горизонтальная (значение) ось.
- Щелкните значок опции оси .
- Откройте раскрывающийся треугольник Параметры оси .
- Внесите изменения в Границы, Единицы и т. д., чтобы настроить шкалу времени для отображения диаграммы в нужном вам порядке.
Возможно, вам придется поиграть с настройками единиц измерения, чтобы ваша шкала показывала нужные вам приращения времени. В этом примере мы хотели, чтобы наши маркеры единиц отображались каждый час, а диаграмма покрывала данные за 24 часа.Итак, наша настройка Unit равна 1/24 или .04167. Значение 0,25 будет отображать маркеры юнитов в 00:00, 6:00, 12:00. и 18:00
Результаты представляют собой четкую, не загроможденную диаграмму, которая равномерно и четко отображает ряд данных за 24-часовой период.
Убедитесь, что для параметра «Тип оси» установлено значение «Ось даты»
Когда вы создаете линейную, столбчатую или гистограмму, Excel автоматически обрабатывает данные даты как «ось дат».
 Это означает, что каждая точка данных будет нанесена на ось X на основе линейного времени, а не на равном расстоянии друг от друга.
Это означает, что каждая точка данных будет нанесена на ось X на основе линейного времени, а не на равном расстоянии друг от друга.Чтобы следовать нашему примеру, загрузите excel time chart.xlsx, лист линейных диаграмм
AB–Text показывает, что ось X установлена на Ось текста , а точки данных равномерно распределены по диаграмме, даже если даты не совпадают в течение всего месяца.
AB–Date показывает, что ось X установлена на Ось даты , а точки данных расположены дальше или ближе друг к другу в зависимости от того, когда данные записывались в течение месяца. Если AB представляет собой снятие средств с банковского счета, в AB-Date вы можете легко увидеть, что больше транзакций происходит в середине и конце месяца.Выполните описанные выше шаги, чтобы открыть параметры оси , чтобы установить для оси X значение оси даты , если диаграмма Excel по умолчанию не делает этого.


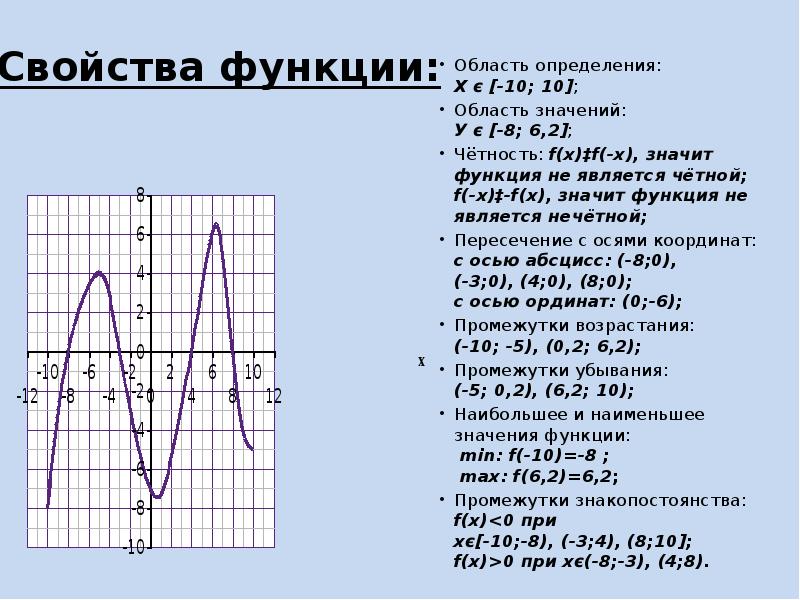
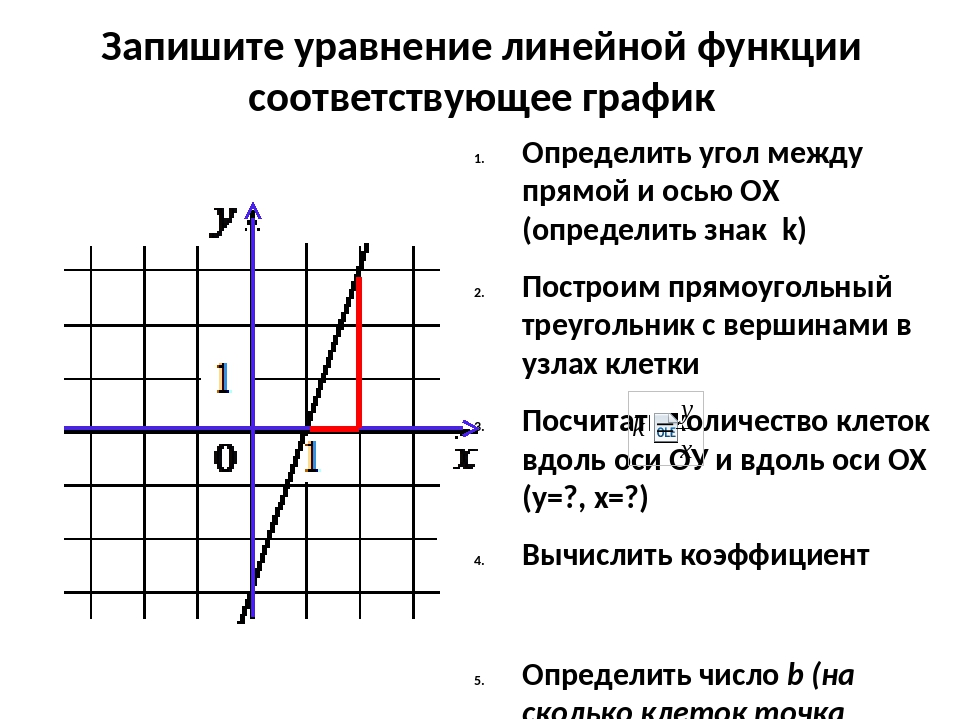

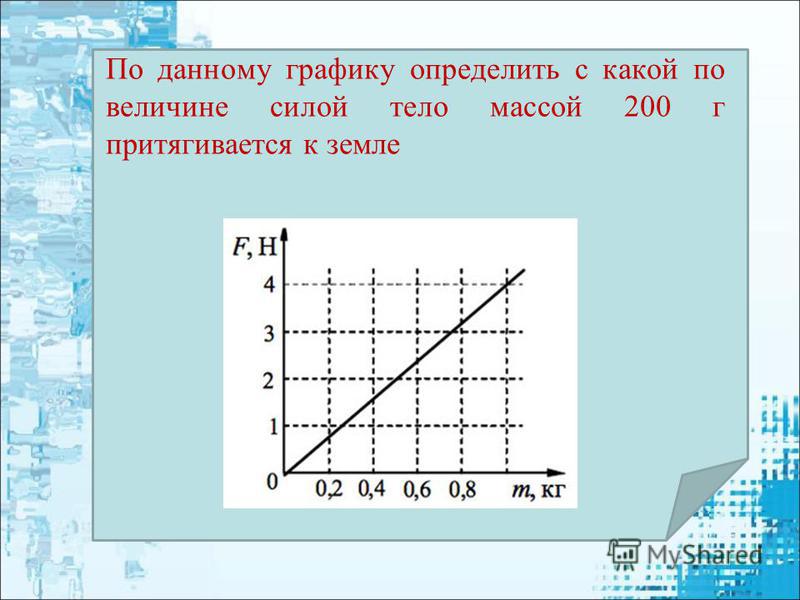

 )
) Мы нажали оба в этом примере. Введите названия осей. В этом примере мы добавили заголовки «Год» (по горизонтали) и «Прибыль» (по вертикали).
Мы нажали оба в этом примере. Введите названия осей. В этом примере мы добавили заголовки «Год» (по горизонтали) и «Прибыль» (по вертикали).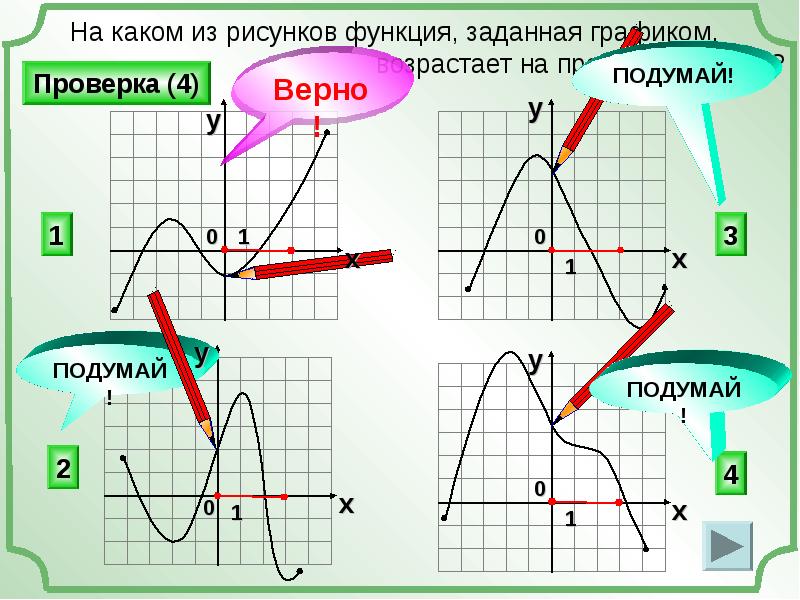 Существует шесть вариантов меток данных: Нет (по умолчанию), Центр, Внутренний конец, Внутреннее основание, Внешний конец, и Дополнительные параметры заголовка метки данных .
Существует шесть вариантов меток данных: Нет (по умолчанию), Центр, Внутренний конец, Внутреннее основание, Внешний конец, и Дополнительные параметры заголовка метки данных .
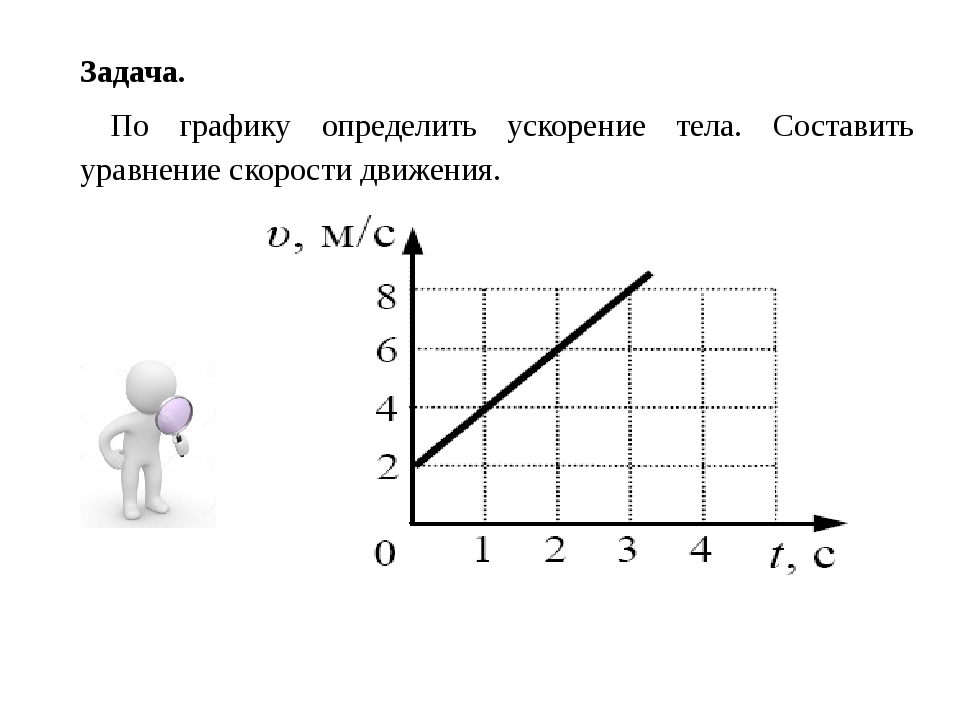
 В дополнение к Дополнительные параметры легенды существует пять вариантов размещения легенды: Нет, Справа, Сверху, Слева и Снизу .
В дополнение к Дополнительные параметры легенды существует пять вариантов размещения легенды: Нет, Справа, Сверху, Слева и Снизу . Отметьте подходящий вариант для вашего набора данных. В этом примере мы нажмем Linear .
Отметьте подходящий вариант для вашего набора данных. В этом примере мы нажмем Linear .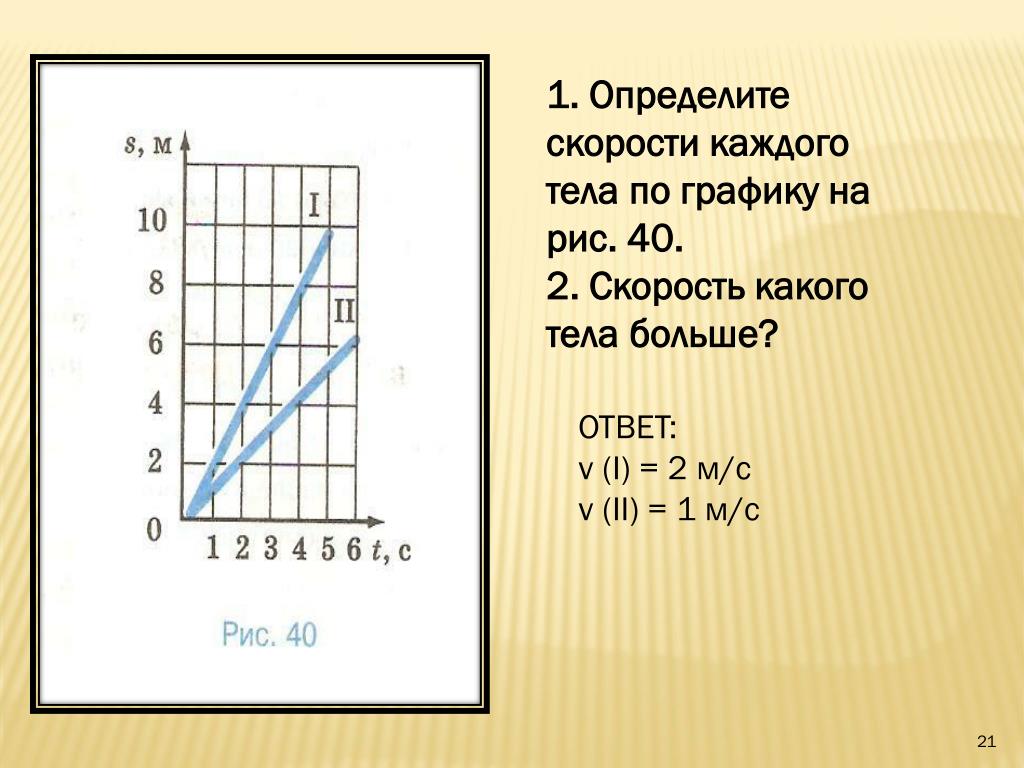

 Выбор ячеек A1:F6
Выбор ячеек A1:F6 Чтобы добавить элемент диаграммы, щелкните команду Добавить элемент диаграммы на вкладке Дизайн , затем выберите нужный элемент из раскрывающегося меню.
Чтобы добавить элемент диаграммы, щелкните команду Добавить элемент диаграммы на вкладке Дизайн , затем выберите нужный элемент из раскрывающегося меню. Например, Excel позволяет переупорядочивать данные диаграммы, изменять тип диаграммы и даже перемещать диаграмму в другое место в рабочей книге.
Например, Excel позволяет переупорядочивать данные диаграммы, изменять тип диаграммы и даже перемещать диаграмму в другое место в рабочей книге.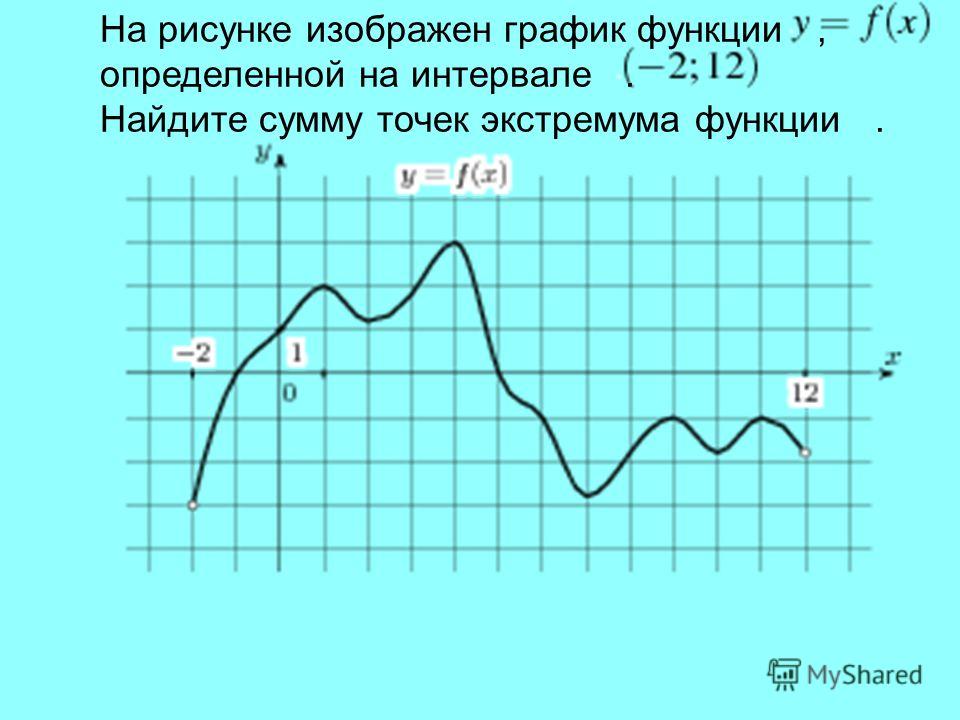 Щелкните команду Switch Rows/Columns
Щелкните команду Switch Rows/Columns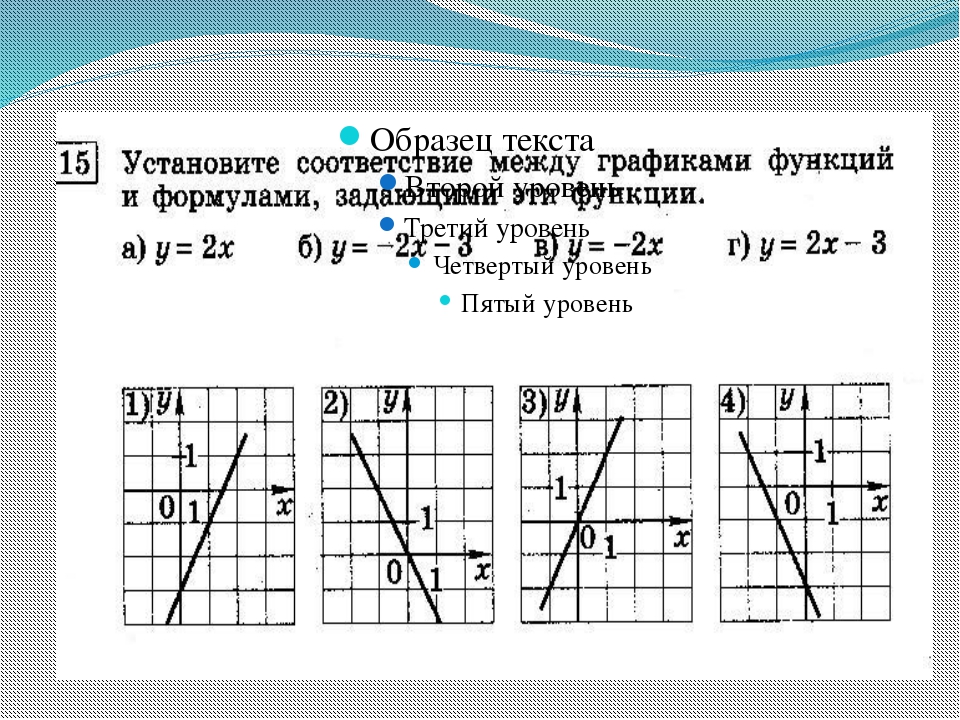 В нашем примере линейная диаграмма упрощает просмотр тенденций в данных о продажах с течением времени. Новый тип диаграммы
В нашем примере линейная диаграмма упрощает просмотр тенденций в данных о продажах с течением времени. Новый тип диаграммы Перемещение диаграммы на новый рабочий лист
Перемещение диаграммы на новый рабочий лист

 В видео я использовал Excel 2021 версии 16.49 для Max OS X.
В видео я использовал Excel 2021 версии 16.49 для Max OS X.

 См. полученную гистограмму ниже.
См. полученную гистограмму ниже. Здесь вы можете изменить цвет заливки легенды, что, в свою очередь, изменит цвет самих столбцов.Чтобы отформатировать другие части диаграммы, щелкните их по отдельности, чтобы открыть соответствующее окно «Формат».
Здесь вы можете изменить цвет заливки легенды, что, в свою очередь, изменит цвет самих столбцов.Чтобы отформатировать другие части диаграммы, щелкните их по отдельности, чтобы открыть соответствующее окно «Формат».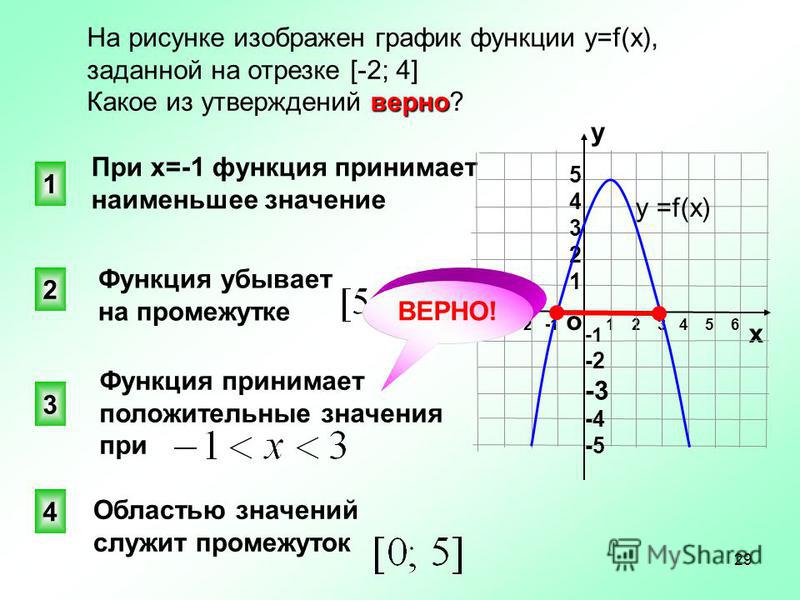 Здесь вы можете решить, хотите ли вы отображать единицы, расположенные на вкладке «Параметры оси», или хотите ли вы изменить, показывает ли ось Y проценты с 2 знаками после запятой или с 0 знаками после запятой.
Здесь вы можете решить, хотите ли вы отображать единицы, расположенные на вкладке «Параметры оси», или хотите ли вы изменить, показывает ли ось Y проценты с 2 знаками после запятой или с 0 знаками после запятой.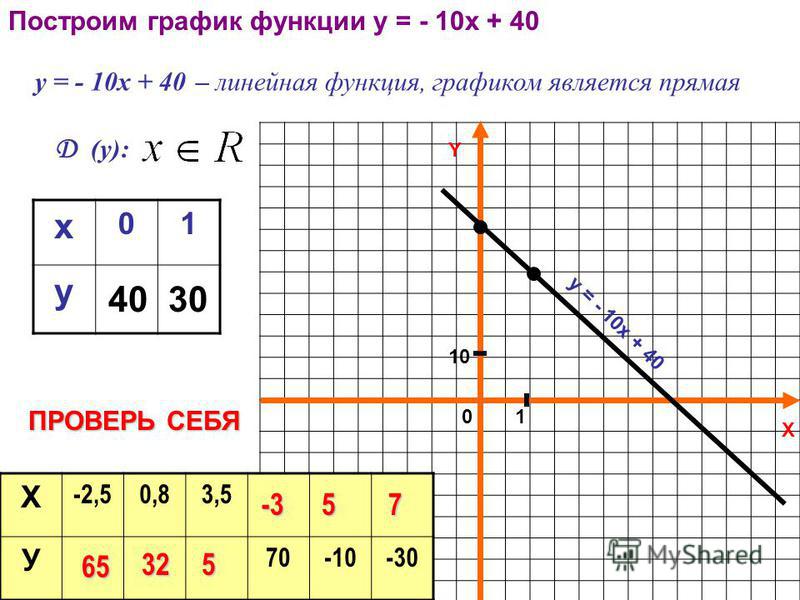 На этот раз щелкните стрелки вверх и вниз, как показано ниже, чтобы изменить порядок данных на диаграмме.
На этот раз щелкните стрелки вверх и вниз, как показано ниже, чтобы изменить порядок данных на диаграмме.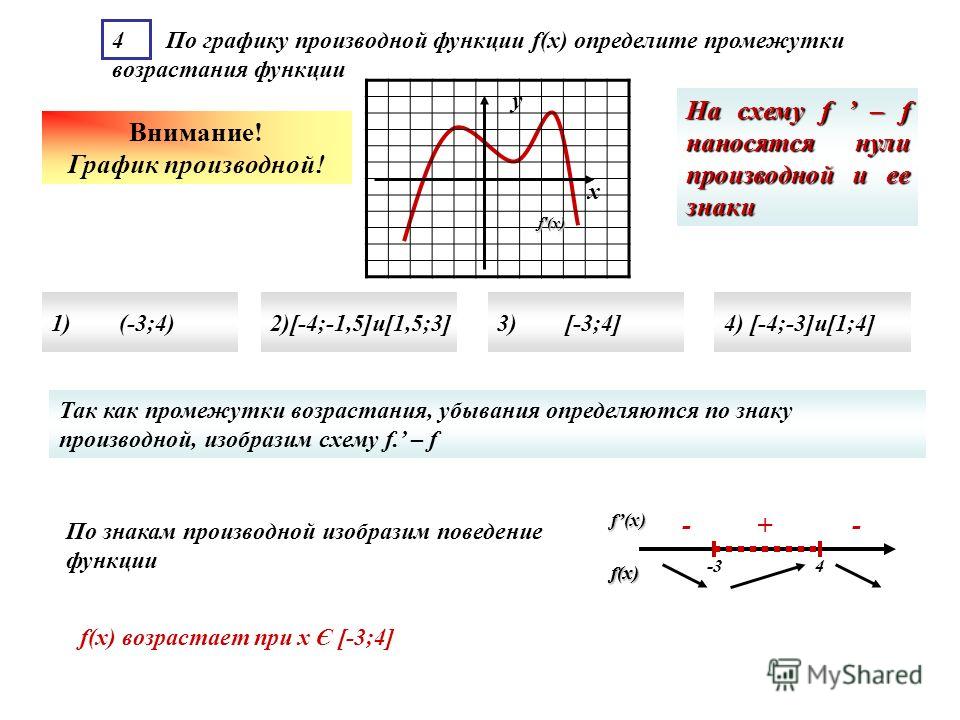 Затем вы можете свободно настроить заголовок диаграммы.
Затем вы можете свободно настроить заголовок диаграммы.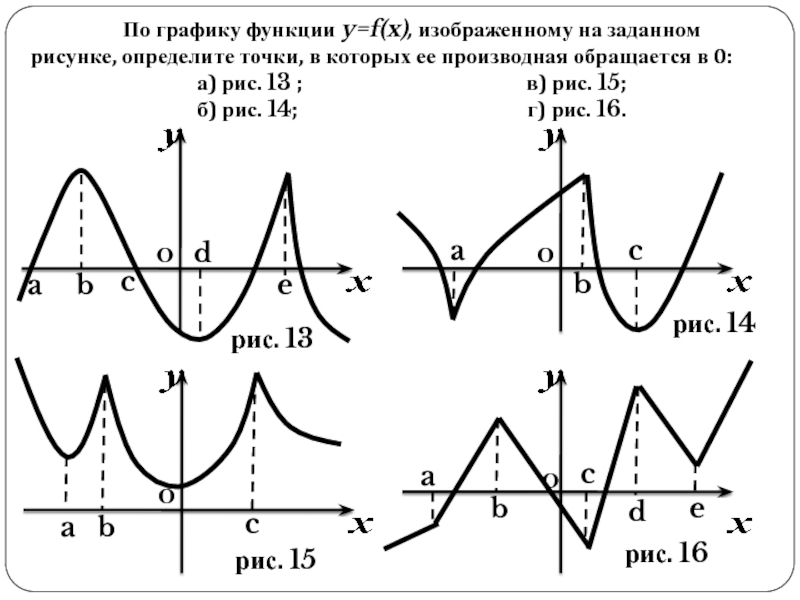 В этом примере я сохраняю его в формате JPEG в папку на рабочем столе.Наконец, нажмите Сохранить.
В этом примере я сохраняю его в формате JPEG в папку на рабочем столе.Наконец, нажмите Сохранить. И хотя вы могли бы написать о них абзац, гораздо интереснее создать диаграмму, чтобы показать вашу информацию.
И хотя вы могли бы написать о них абзац, гораздо интереснее создать диаграмму, чтобы показать вашу информацию. Есть числовые диаграммы, а также организационные диаграммы, которые помогут вам визуализировать мысли и идеи.
Есть числовые диаграммы, а также организационные диаграммы, которые помогут вам визуализировать мысли и идеи.


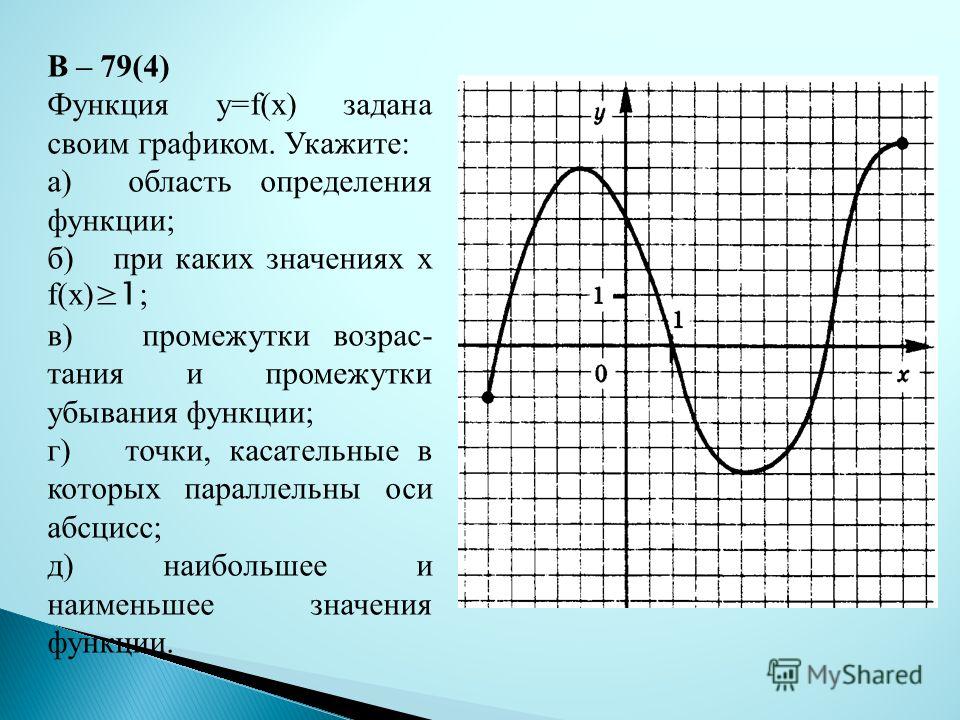


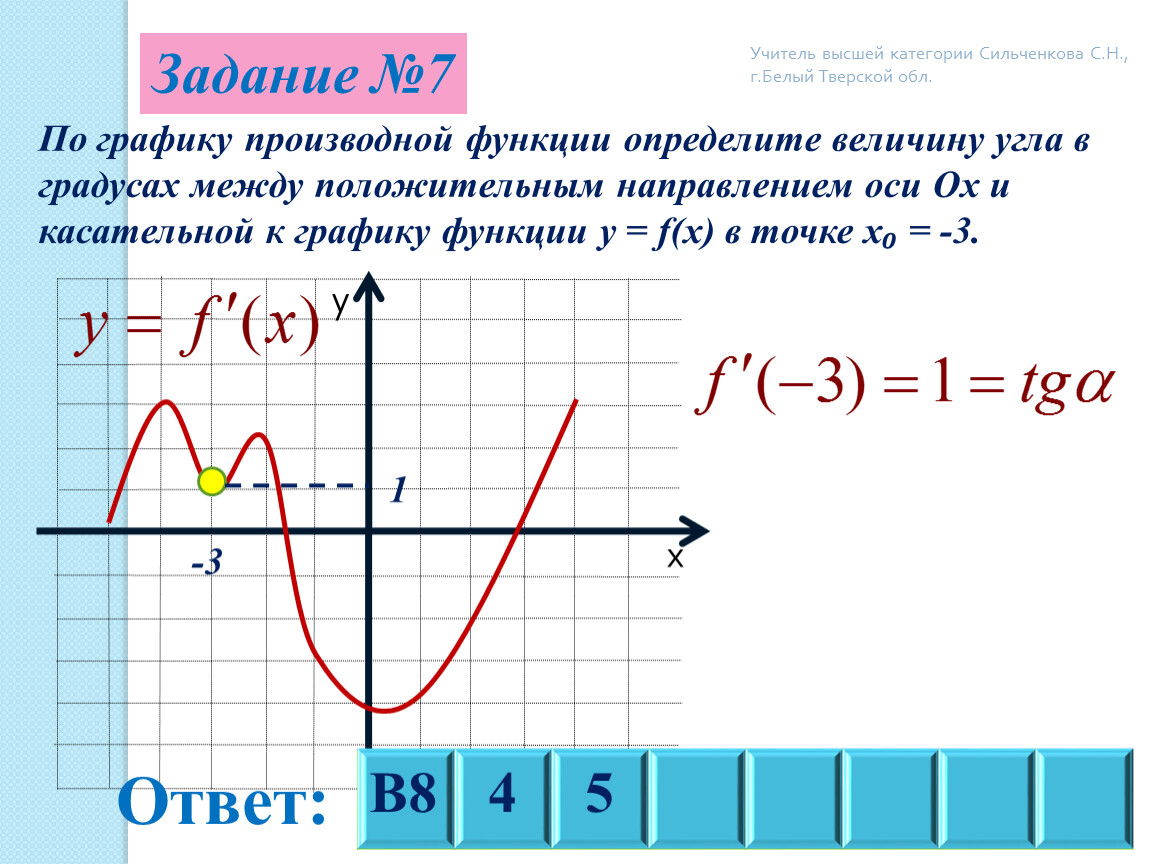
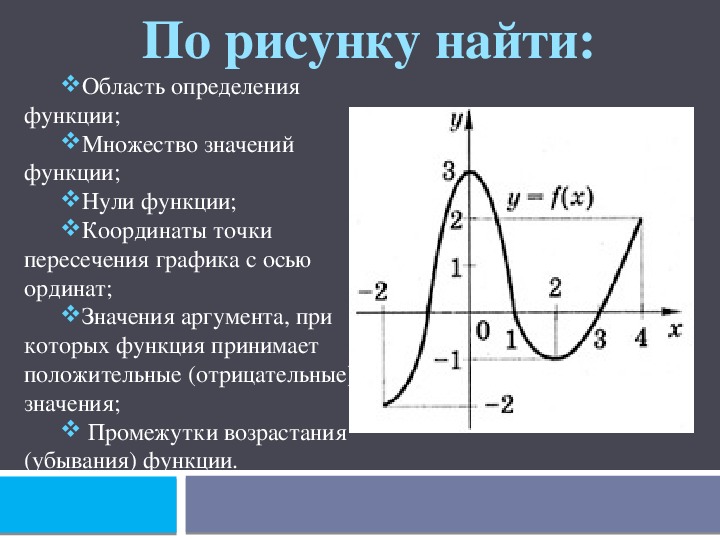



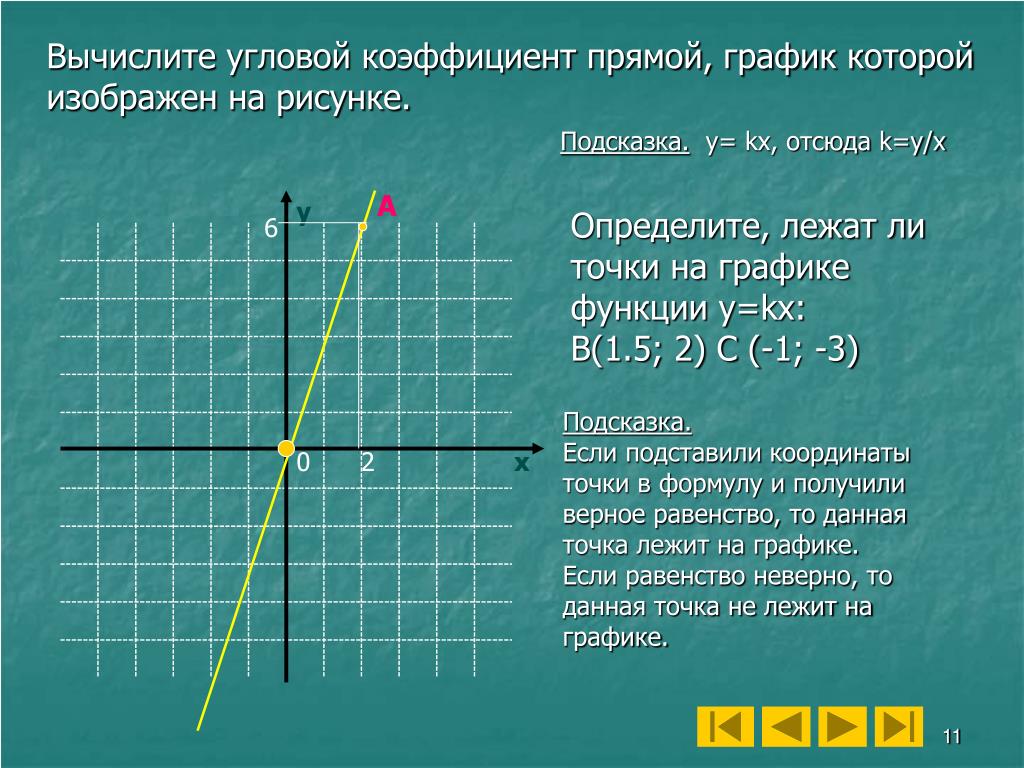
 Если вы создаете диаграмму для определения частоты или корреляции, например, в случае гистограммы или точечной диаграммы, ваши результаты зависят от того, где они находятся на каждой оси.
Если вы создаете диаграмму для определения частоты или корреляции, например, в случае гистограммы или точечной диаграммы, ваши результаты зависят от того, где они находятся на каждой оси.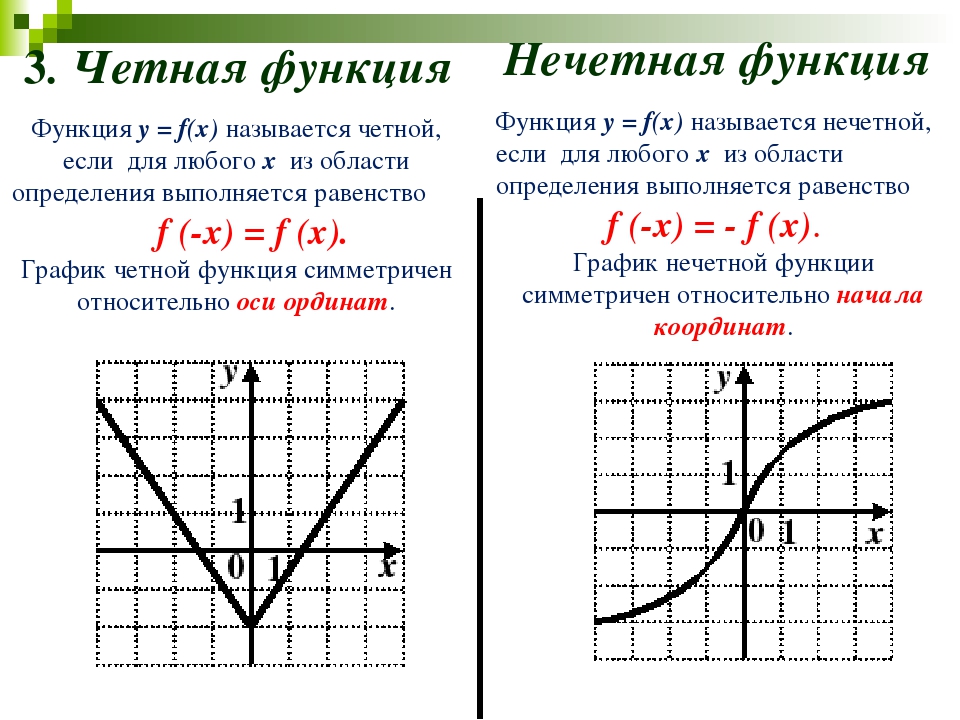
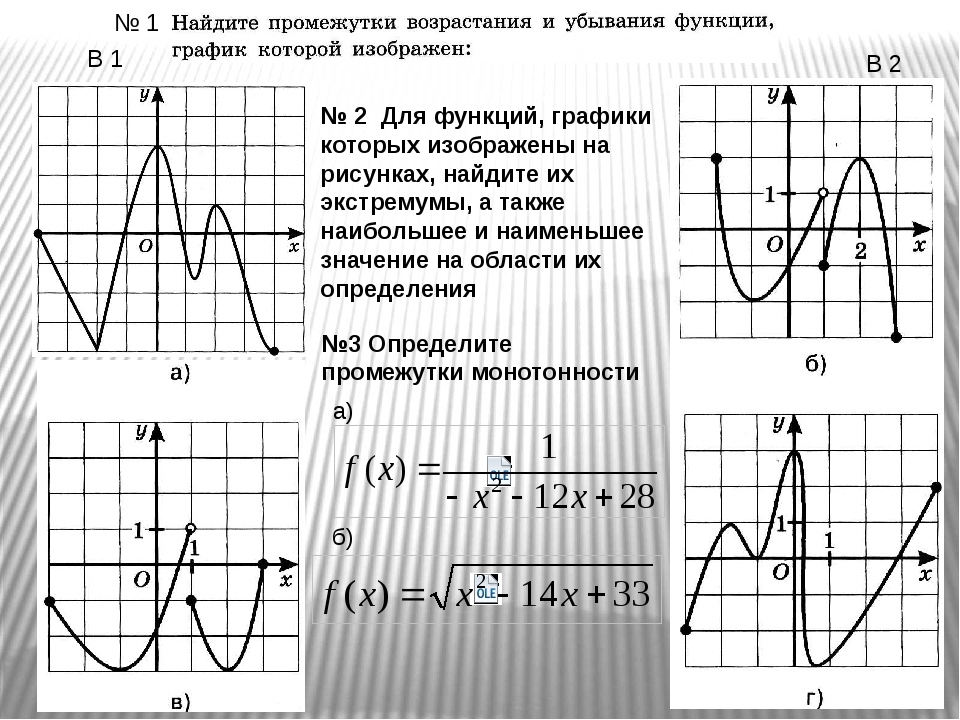
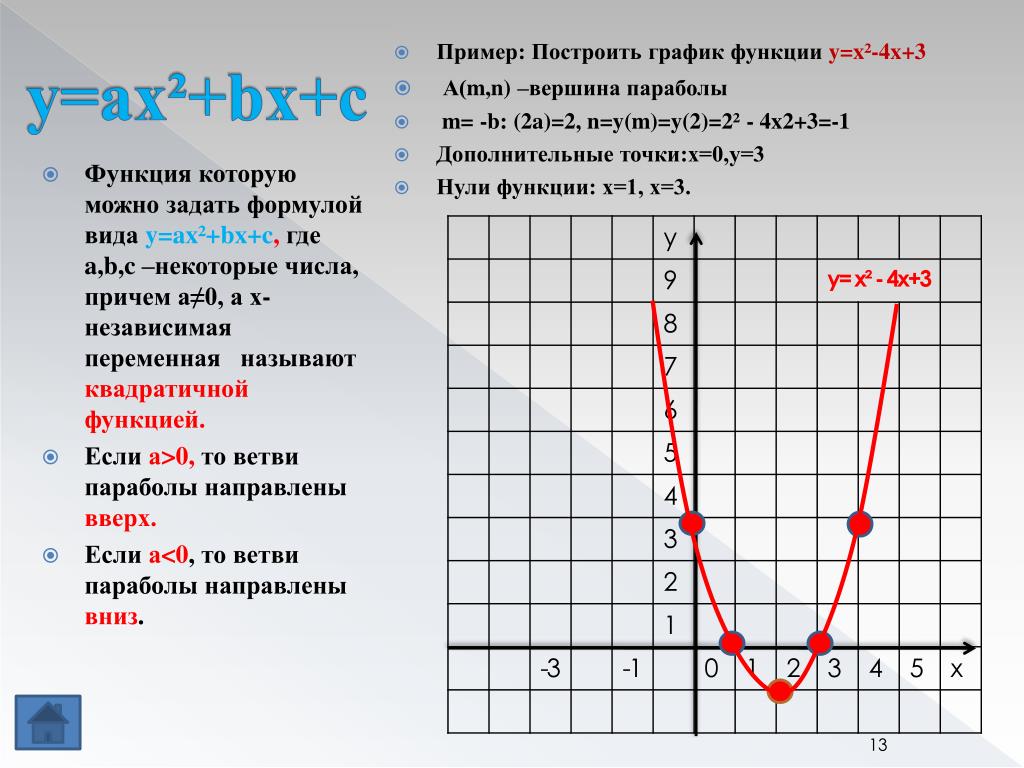




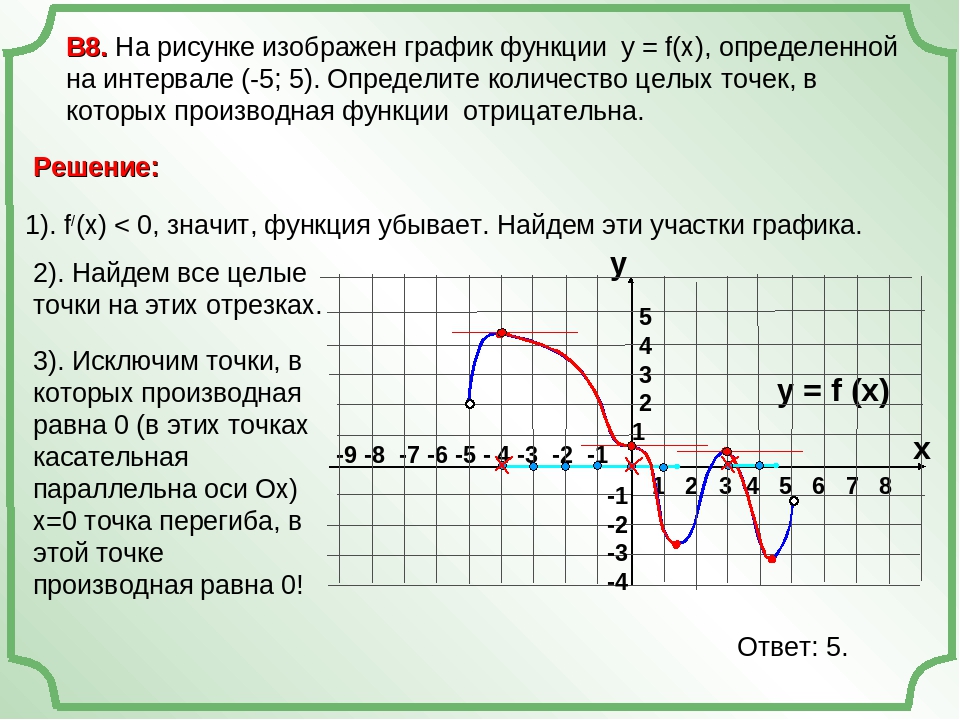
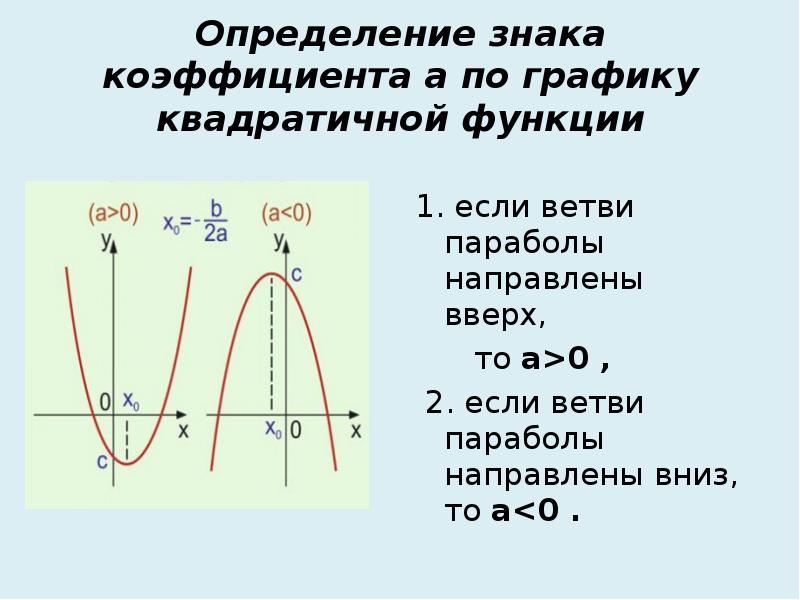 С этими диаграммами у вас будет широкий набор инструментов для удовлетворения ваших потребностей в визуализации данных. Рекомендации о том, когда выбирать каждый из них в зависимости от варианта использования, описаны в следующей статье.
С этими диаграммами у вас будет широкий набор инструментов для удовлетворения ваших потребностей в визуализации данных. Рекомендации о том, когда выбирать каждый из них в зависимости от варианта использования, описаны в следующей статье.
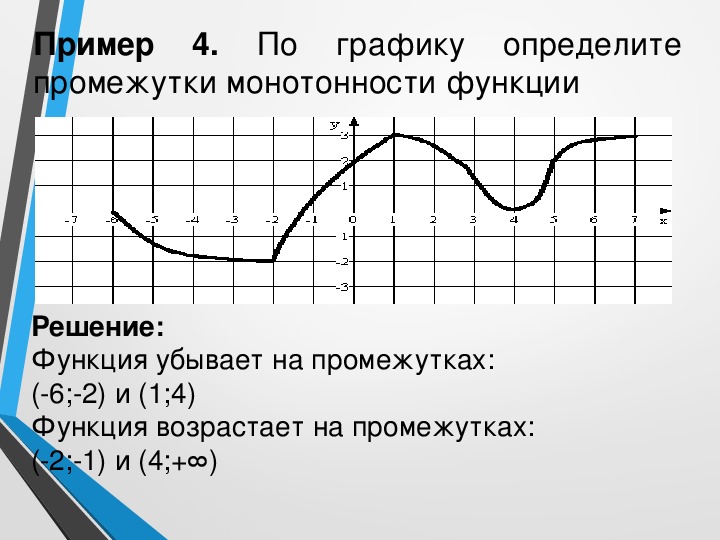
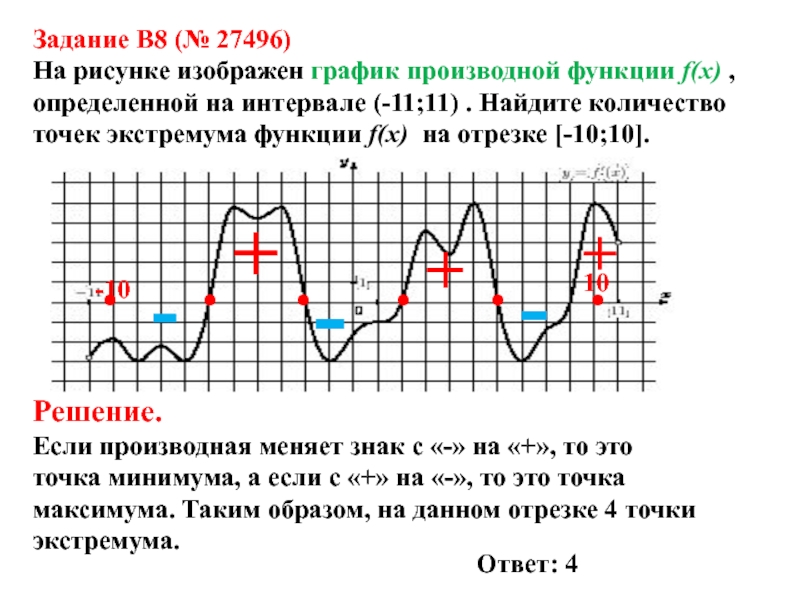 Вторичные кодировки, такие как площадь, форма и цвет, могут быть полезны для добавления дополнительных переменных к более простым типам диаграмм.
Вторичные кодировки, такие как площадь, форма и цвет, могут быть полезны для добавления дополнительных переменных к более простым типам диаграмм.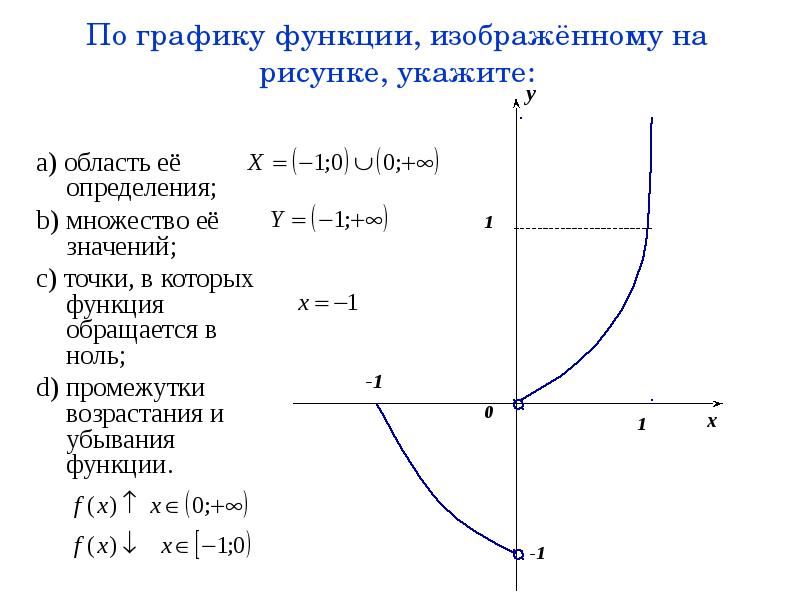
 Эту диаграмму чаще всего можно увидеть в сочетании с концепцией суммирования, чтобы показать, как сумма изменилась с течением времени, а также как изменились вклады ее компонентов.
Эту диаграмму чаще всего можно увидеть в сочетании с концепцией суммирования, чтобы показать, как сумма изменилась с течением времени, а также как изменились вклады ее компонентов.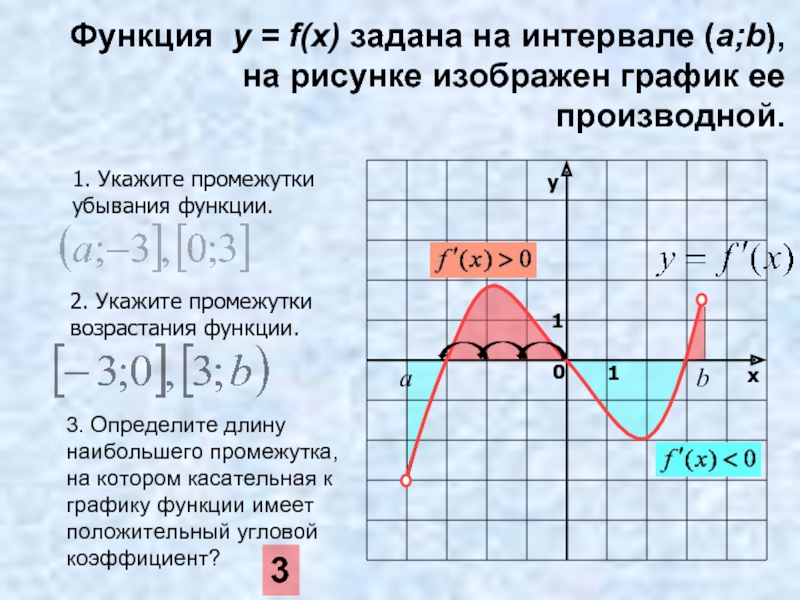 Если точки данных каким-то образом упорядочены, точки также можно соединить с отрезками, чтобы показать последовательность значений. Когда третья переменная является числовой по своей природе, именно здесь появляется пузырьковая диаграмма. Пузырьковая диаграмма строится на основе диаграммы рассеяния, когда значение третьей переменной определяет размер каждой точки.
Если точки данных каким-то образом упорядочены, точки также можно соединить с отрезками, чтобы показать последовательность значений. Когда третья переменная является числовой по своей природе, именно здесь появляется пузырьковая диаграмма. Пузырьковая диаграмма строится на основе диаграммы рассеяния, когда значение третьей переменной определяет размер каждой точки.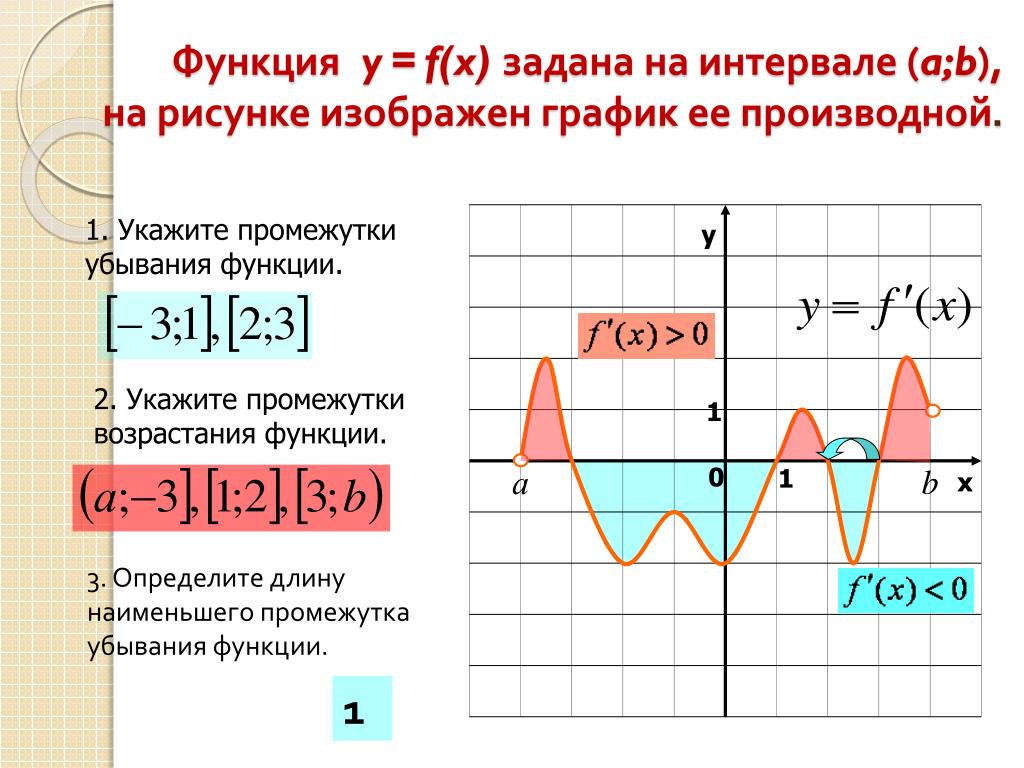 На скрипичном графике каждый набор прямоугольников и усов заменяется кривой плотности, построенной вокруг центральной базовой линии.Это может обеспечить лучшее сравнение форм данных между группами, хотя и теряется при сравнении точных статистических значений. Частой вариацией для скрипичных сюжетов является добавление маркировки в виде прямоугольника поверх скрипичного сюжета, чтобы получить лучшее из обоих миров.
На скрипичном графике каждый набор прямоугольников и усов заменяется кривой плотности, построенной вокруг центральной базовой линии.Это может обеспечить лучшее сравнение форм данных между группами, хотя и теряется при сравнении точных статистических значений. Частой вариацией для скрипичных сюжетов является добавление маркировки в виде прямоугольника поверх скрипичного сюжета, чтобы получить лучшее из обоих миров.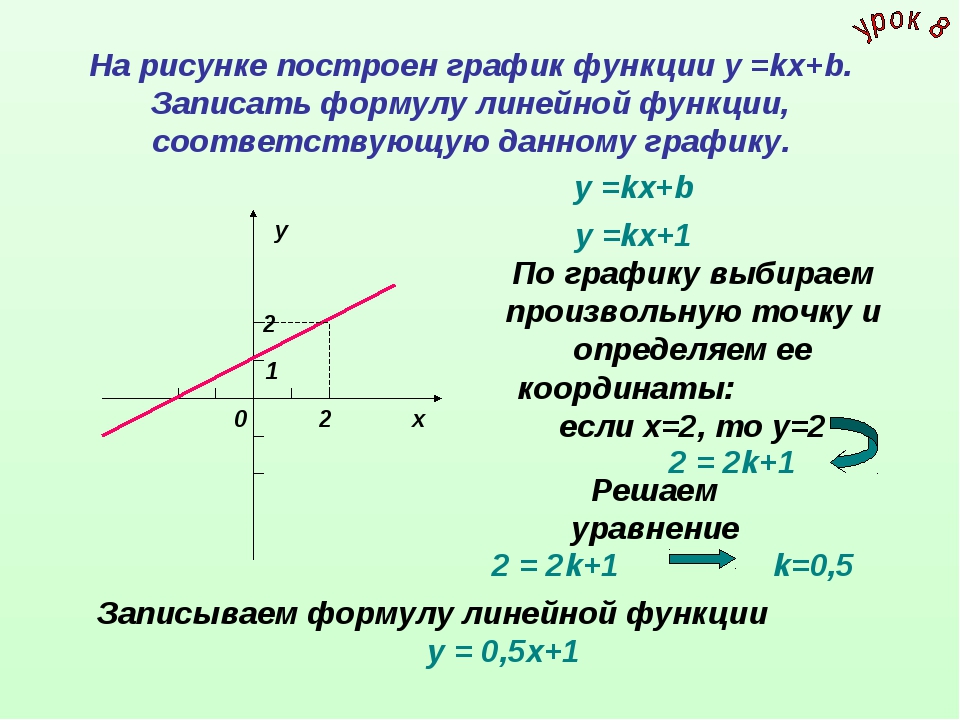
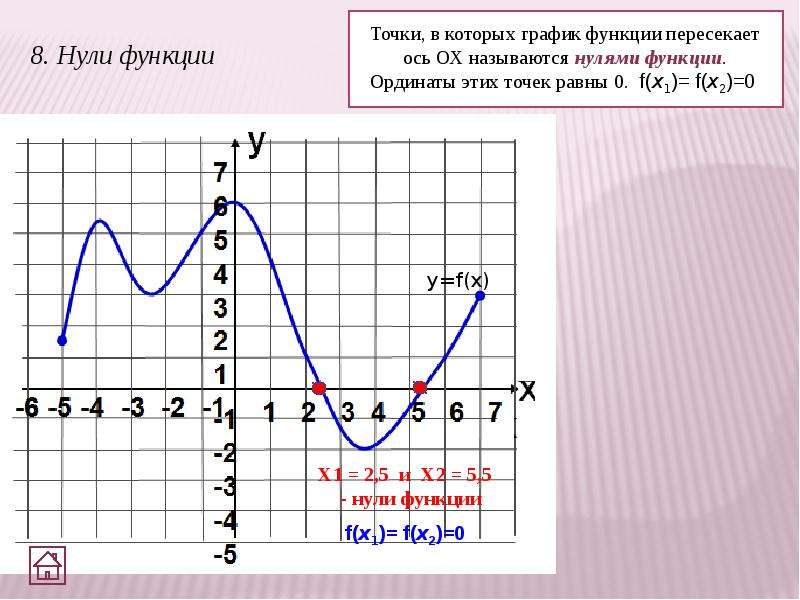

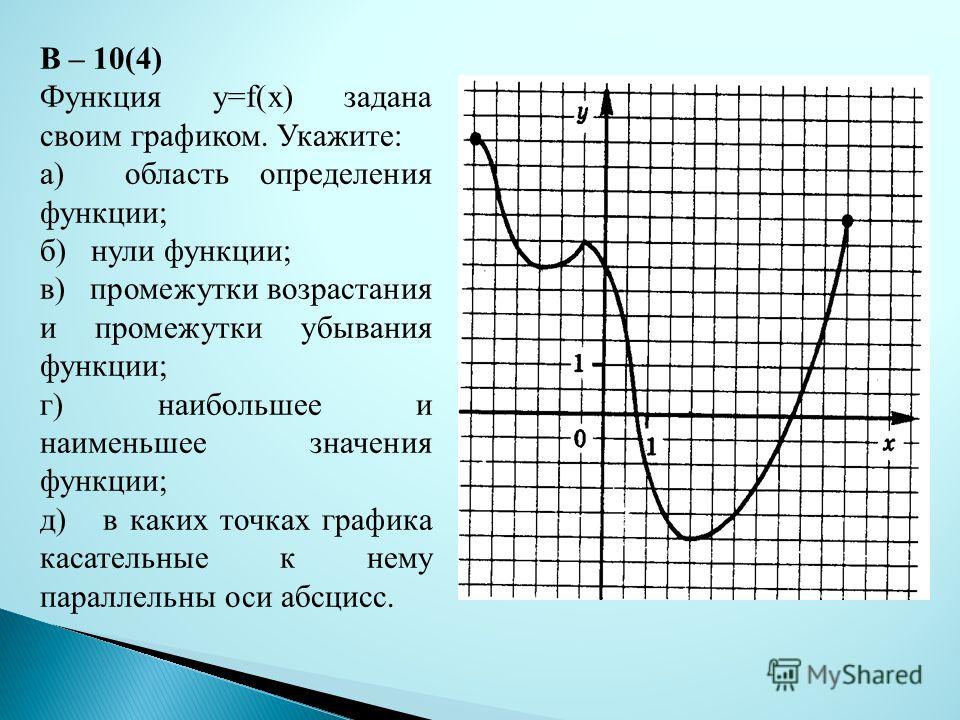 Вот несколько советов по редактированию данных о времени и дате в диаграмме Excel. Эти функции применимы к Excel 2007–2013, хотя конкретные шаги зависят от вашей версии.Изображения были сделаны с использованием Excel 2013 в ОС Windows 7.
Вот несколько советов по редактированию данных о времени и дате в диаграмме Excel. Эти функции применимы к Excel 2007–2013, хотя конкретные шаги зависят от вашей версии.Изображения были сделаны с использованием Excel 2013 в ОС Windows 7.
 Это означает, что каждая точка данных будет нанесена на ось X на основе линейного времени, а не на равном расстоянии друг от друга.
Это означает, что каждая точка данных будет нанесена на ось X на основе линейного времени, а не на равном расстоянии друг от друга.