Магазин Toy&Toy — Super Toys

Быки и коровы правила игры

Быки и коровы — логическая игра для двоих игроков. Для неё достаточно иметь листок бумаги и ручку, свободное время и немного везения. Как правило, такое время находится у школьников и студентов. Но мне, вашему покорному слуге, не довелось в свои годы узнать эту забаву. Хотя почему бы не размять своё серое вещество на досуге? Это неплохая тренировка для ума, не требующая сильного напряжения, и как развлечение вполне себя оправдывает.

В своём классическом варианте правила очень просты и не притязательны. Играют два человека, каждый загадывает в тайне от оппонента четыре цифры без повторений. Например, это может быть число 0834. Ноль является также цифрой и вполне может быть на первом месте.

Далее игроки по очереди делают ходы, то есть пытаются угадать задуманное противником число. Но спрашивать они обязаны так же в виде четырёхзначного числа. К примеру нас спросят: «Твоё число 3094?». В ответ же мы должны сообщить количество быков и коров. Бык — это цифра, которая есть в нашем загаданном числе и находится на той же позиции. А корова — это цифра, которая так же есть в нашем числе, но находится не на своём месте. В нашем случае получаем две коровы, это цифры 3 и 0, и один бык, это 4. Теперь будем спрашивать мы, и так далее, до тех пор, пока кто-либо не разгадает полностью число. То есть в ответе он получит четыре быка. На картинке показан пример игры. Времени на одну партию требуется совсем немного. На практике обычно требуется от 5 до 8 ходов, но есть уникумы, которые умудряются и за три хода победить. Конечно в таком успехе есть немалая доля везения.

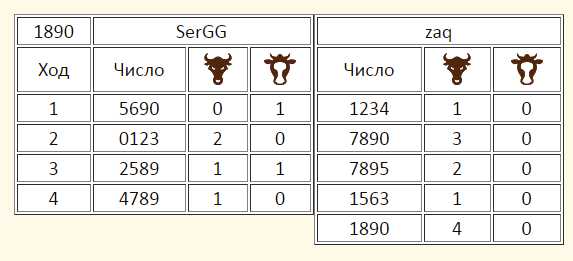
На нашем сайте Вы можете играть в «быки и коровы» как против компьютера, так и онлайн с живым противником. Внизу игровой комнаты для Вашего удобства есть игровой чат, в котором можно подобрать себе противника для игры по сети, либо спросить совета. Так же если у Вас есть замечания по реализации нашей игры, предложения по её улучшению или развитию — то пишите нам. Можно писать как на форуме, так и нам на почту mail@Робомозг.рф.

Разновидности игры

Вариантов игры великое множество:

• 1. По типу угадываемой последовательности — это может быть число. В классике — это четырёхзначное без повторений, состоящее из цифр от 0 до 9. Так же может увеличиваться количество цифр в числе, возможность их повторения. В качестве последовательности могут использоваться цвет, какая либо криптограмма, слово.
• 2. По типу самой игры. В эпоху компьютеров появилась возможность играть одному. Когда человек угадывает число, задуманное компьютером, либо против компьютера. Но машину трудно победить, тут больше вопрос правильно заложенного алгоритма в неё. Игроки играют в классический вариант, но находятся на значительном удалении друг от друга. Игроки угадывают по очереди число, которое задумал компьютер — тут возможны варианты как так называемого горячего стула, когда оппоненты находятся рядом и играют за одним компьютером, так и удалённо.

На данный момент реализован только классический вариант игры. Если у Вас есть идеи, какой вариант быков и коров должен появиться на нашем сайте, то поделитесь ими с нами.

xn--90aeltibbl.xn--p1ai

Игра «Быки и коровы» и «Математические карты»

Разделы: Начальная школа

---

Игра “Быки и коровы”

Игра “БЫКИ–КОРОВЫ” — замечательная логическая игра, не требующая специальных приспособлений. В нее можно играть в любых ситуациях: дома, на даче, в поездках и даже в ожидании очередей.

Игра развивает умение сравнивать и анализировать.

Играют двое. Каждый загадывает число из четырех неповторяющихся цифр (ноль в игре используется, но на первом месте стоять не может).

Задача противника отгадать число из 10 попыток.

Противник называет любое 4-хзначное число, у которого цифры также не повторяются Его необходимо написать под своим загаданным числом, чтобы было удобно сравнивать цифры. При совпадении цифр названного числа с загаданным говорится “БЫК”.

Бык означает, что цифра отгадана и стоит в нужной позиции (например, в задуманном числе первая цифра 3 и в названном противником – тоже первая 3 – это бык.). Корова означает, что цифра отгадана, но она стоит не в своей позиции. Путем логических рассуждений и проверки ответов необходимо угадать все 4 цифры числа и их порядок. Выигрывает тот, кто первым угадает число противника. Например, загадано 3749 и победитель называет 3749.

Игра с числами на самом деле не очень сложна, так как цифр всего 10 и повторяться они не могут. Ее могут освоить дети даже 8-9 лет.

Пример игры:

3749 – загаданное число

3589 – называет противник – ваш ответ – 2 быка. (3 и 9 стоят на своих местах)

7628 – называет противник – ваш ответ – 1 корова. (только 7 есть в числе, но не на своем месте).

Значит, из первого числа используются 2 цифры, а из второго только одна (но какие после первого ответа определить невозможно). Дальше, называя следующие числа, надо вычислить сами цифры и их порядок.

По двум ответам определить используется ли цифра 8 в загаданном числе нельзя – надо пробовать другие числа и сравнивать, какой ответ получаешь. Например, 8601 – ни одной цифры в загаданном числе нет. Значит, и в первом, и во втором числе цифры 6 и 8 можно зачеркнуть и дальше пробовать числа без этих цифр.

4973 – называет противник – ваш ответ – 4 коровы (т.е. все цифры правильные, а вот их порядок – нет). А вот ответ: 3 быка 1 корова быть не может, так как если три цифры стоят на своем месте, то и четвертая – тоже.

ИГРА “Быки и коровы” со словами

После освоения игры с числами интереснее перейти на игру со словами.

В русском языке очень много слов из 4 букв (играем всегда в значащие слова). А сочетание букв могут быть самые разные: и 3 согласных 1 гласная, и 2 на 2, и 1 на 3. Не используется только твердый знак и слова типа МАМА, ФАРА, РАМА, ОКНО, ТОРТ и т.д., где 2 одинаковые буквы. Принцип игры остается тем же: буква на своем месте –

бык, буква есть в слове, но не на своем месте, — корова.

Играть можно на любом клочке бумаги, годится даже пол-листочка или исписанный с одной стороны, а заставляет сравнивать и логически мыслить, так как надо все время заниматься перестановками и анализом – где же все-таки бык и какой он? Например, противник может загадать и пруд, и прут, и порт – и замена даже одной буквы приводит уже к новому слову, а иногда одни и те же буквы могут быть в разном порядке – и будет два разных слова, например, лето и тело. Себе на листочке сбоку для подсказки удобно выписывать алфавит и проверять разные варианты подстановки букв (

тень, день, пень, лень…..)

Примеры игры:

* * * * рука – 1 к слон – пусто (нет ни одной буквы) гриб – 3 б горб – 1 б 1 к бусы – пусто грим – 3 б гриф – слово угадано.

* * * * луна – 1 б море – 1 к угол – 1 к порт – 1 к нора – 1 к стул – 1 к лень – пусто буря – 1 б 2 к рука – 1 б 1 к сруб – 3 к шуба – 2 б зубр – слово угадано.

Математические карты

Игра позволяет тренировать устный счет и таблицу умножения. Рекомендуется для учащихся начальной школы.

Делаются они так: берутся два набора чисел от 1 до 24 (для чисел удобно использовать старый настенный календарь). Всего 48 карт. На каждой карте (основа – картон) делается одно число в двух противоположных углах, чтобы тому, кто сидит напротив, было удобно смотреть на это же число (см. рисунок).

Правила: Каждому играющему дается по 4 карты. Начинающему игру дается пятая карта. Из своих 5 карт он выбирает одну, которую дает соседу в качестве задания.

Принцип игры такой: игрок из своих 4 карт, то есть чисел, используя любые математические действия: +, — , *, : (сложение, вычитание, умножение, деление) и ставя числа в любом(!) порядке, должен получить ответ, который дал ему сосед. Те числа-карты, которые он при этом использовал вместе с ответом, игрок берет себе как «взятку». А в конце игры каждый считает, сколько он набрал карт в своей стопочке. Эта игра рассчитана на тренировку устного счета, простейшего деления и умножения (все варианты до 24).

Например: первому игроку достались карты: 17, 4, 8, 9. А в качестве задания дали сделать 10 или 16.

• число10 получается очень легко: 8:4+17-9=10;
• число 16 сделать уже сложнее: (17-9)*(8:4)=16.

А если «поиграть» с этими числами, то можно получить еще целый набор ответов: 12, 14, 13, 23, 6, 4, 20… Например, 12 = 17 – 4 – (9 — 8). 14 = 17 – 4 + (9 – 8).

Преимущество игры в том, что последовательность чисел и математических действий не фиксирована, как в учебнике математики, а играющий сам должен определить их, перекладывая карточки в любом порядке, а также то, что игра ведется в открытую и все играющие тоже “ломают голову”, чтобы решить данный пример.

Если скобки используются при записи примера, то устно можно про них ничего не говорить, просто называть действия в нужном порядке: для 16 (из примера выше): сначала из 17 вычитаю 9, получается 8; 8 делю на 4, и 8 умножаю на 2. Очень часто есть несколько вариантов получения ответа.

Иногда, конечно, бывает такая ситуация, когда ответ ну никак не получается, тогда взрослый проверяет это и просит, чтобы поменяли задание или меняет одну карту у игрока из неиспользованной колоды. Иногда решение может быть только из трех карт, тогда игрок берет себе во «взятку» не 5, а 4 карты.

В этой игре дети, например, очень хорошо тренируют простейшее деление и умножение (на 2, на 3, на 4), а также свойство 1: если на нее умножить или разделить — число не изменится.

Рекомендую попробовать и поиграть дома, а также давать набор чисел и результат, который надо получить, как дополнительное задание на уроках математики.

20.09.2016

urok.1sept.ru

Быки и коровы алгоритм игры

Правила игры изложены в отдельной статье, а здесь мы займёмся изучением вопроса оптимального алгоритма поиска числа противника в игре быки и коровы. И так, есть общие принципы как следует задавать вопросы:

• Вопрос должен быть таким, чтобы ответ был максимально информативен.
• Категорически избегаем повторений. Нет нужды спрашивать то, что мы уже знаем.
• Немного везения как никогда будет кстати.

Сколько комбинаций цифр можно составить? Первую цифру можно загадать десятью способами, вторую девятью и тд. И получаем 10*9*8*7 = 5040. Вот это общее количество комбинаций. А вариантов ответов может быть всего 14, они все показаны на рисунке.

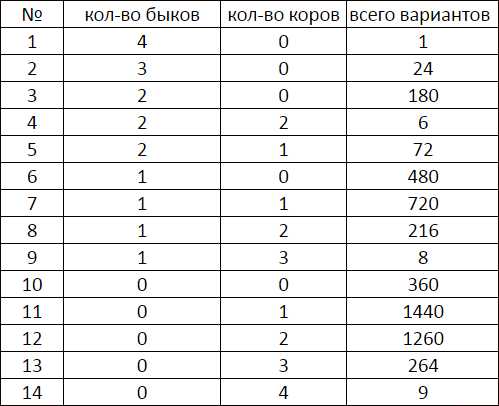
В приведённой таблице рассмотрены все варианты ответов. Самый желанный и вкусный — это 4 быка, то есть сразу выигрыш. И такой вариант один. Самый вариативный это 1 корова — имеет 1440 вариантов расстановки цифр. По большому счёту наши дальнейшие шаги буде определять наш первый ход. А тут мы может положиться только на нашу удачу, расположение звёзд, расставленной мебели по фен-шую и наличию кофе. То есть любую комбинацию цифр. И по полученному ответу мы планируем дальнейшие шаги. Рассмотрим варианты, кроме 4быков:

• 0 быков, 0 коров — это тоже вполне удачный ход! Эти цифры сразу исключаем из угадываемого числа, но можем использовать для выявления быков.
• 1 бык или 1 корова — то есть мы нашли одну цифру, но какая она не ясно.
• 1 бык и 1 корова, или 2 быка или 2 коровы — нашли 2 цифры.
• 3 быка и 0 коров, 2 быка и 1 корова, 1 бык 2 коровы. Нашли 3 цифры, но самый желанный — это три быка, всего 24 комбинации! На практике 4 хода.
• 2 быка и 2 коровы, 1 бык и 3 коровы, 4 коровы — то есть мы нашли все цифры. Здесь мы можем кричать ура, так как выигрыш считайте у нас в кармане! Самое большее 9 комбинаций!

Дальнейшую стратегию рассмотрим на примерах игры, так будет гораздо наглядней и проще.

Первый пример

На первый вопрос 1234 мы получили ответ одна корова. Вторым вопросом была комбинация 5678. И тут удача — два быка и одна корова. Логика третьего хода следующая: мы угадали три цифры, нужно определить их расположение. И мы точно знаем что цифра 9 и 0 отсутствуют в загаданном числе. Потому берём две цифры из второго вопроса, но ставим на другие места и доставляем 0 и 9.

Получаем такой вопрос: 7890, на который мы получили ответ 2 коровы. Поздравляем — мы точно определили 2 быка: 7 на третьем месте, 8 на четвёртом. Далее мы знаем что 5 или 6 точно есть в загаданном числе. Уберём одно и поставим на другое место. Последнее число возьмём из первого вопроса, тут без разницы какое — чистое везение. Получаем такой вопрос — 4578. И радуемся победе, мы отгадали, ответ четыре быка!

Второй пример

На первый вопрос 0123 мы получили ответ 1 бык, 2 коровы. Вторым вопросом задаём 4567. Получаем в ответе 1 корова. Всё, мы снова исключили две цифры — это 8 и 9. И теперь мы возьмём две цифры с первого вопроса и как обычно поставим на другое место, добавим 8 и 9.

Получился такой вопрос 2389, ответ на который был одна корова. Казалось бы результат так себе, но не тут-то было! Скомбинируем третий вопрос так — возьмём ноль с первого вопроса, но менять его место не будем, возьмём двойку с третьего и поставим на второе и разбавим несуществующими. Вот что получили: 0289. Ответом было два быка! Теперь тройку тоже вычеркнем, а это значит, что единичка точно в числе есть. Теперь осталось всего два варианта и мы выбираем 0215. И получаем 4 быка! Пятёрочка — это чистое везение.

Третий пример

В первый раз спросим 9012. Получаем 2 коровы. Второй вопрос — 3456 — тоже две коровы. Так, 7 и 8 исключаем. Теперь перетасовываем второй вопрос и уберём одну, заменив на семерку. Получаем такой вариант : 6573. Ответ — одна корова. Что мы поняли? Цифра 4 точно есть и получили расположения, где цифры 3, 5 и 6 точно не стоят.

Четвёртый вопрос формируем так — комбинируем третий и первый вопрос, меняя местами. Вот какую комбинацию мы получили — 1234. Ответ — три быка. 3 и 4 стоят на своих местах, проверяем только первые цифры. 9234 — ответом на него было 2 быка, одна корова. Всё, мы нашли число! 1934.

Четвёртый пример

Первый вариант у нас 4590, ответ — один бык. Второй ход 1236 и ответ три коровы. Снова 7 и 8 вне игры. На третьем ходу тасуем цифры третьего вопроса и разбавляем 7. 7263, что даёт нам снова 3 коровы. Значит единичку выбрасываем.

Теперь нам нужно правильно расположить наших коров и найти быка с первого вопроса. Задаём такой вариант — 4623, ответ на него два быка и одна корова. Значит не четвёрка. Тройку мы не меняли и потому точно можем сказать, что именно тройка не на своём месте! Пробуем ещё раз — 3620. И бинго!!!! Мы разгадали число!

Бытует мнение, что выявив цифры, которые точно отсутствуют в загаданном числе, то их использовать дальше нельзя. И следует оперировать только найденными коровами, чтобы найти быков. Я придерживаюсь другого мнения. «Пустышки» крайне полезны в выявлении быков, так как мы можем точно определить цифры, которые стоят на своих местах. И это не будет какой либо потерей хода. Наоборот, оперируя только найденными коровами можно запутаться в том, какая из коров в данный момент стала быком.

Я старался в кратце описать ход своих мыслей при игре в быков и коров. Конечно, у каждого свой стиль игры. и многое зависит от везения. И на последок, удачи Вам и приятной игры.

xn--90aeltibbl.xn--p1ai

Разработка оптимальной стратегии игры «Быки и коровы» на основе теории информации

Когда я поступил в институте, очень популярной была игра «Быки и коровы». Так совпало, что в это же время я прочитал математическую новеллу Альфреда Реньи «Дневник. – Записки студента по теории информации». Благодаря этой статье я познакомился с основами теории информации. И у меня родилась идея, как улучшить свои показатели в «Быках и коровах», опираясь на новые знания [1].

Кратко напомню правила. Играют двое. Каждый задумывает и записывает тайное 4-значное число с неповторяющимися цифрами (первой может быть и ноль). Игрок, который начинает игру по жребию, делает попытку отгадать число. Попытка — это 4-значное число с неповторяющимися цифрами, сообщаемое противнику в виде вопроса. Противник говорит в ответ, сколько цифр угадано с совпадением их позиций в тайном числе и сколько угадано без совпадения. Например: задумано тайное число 3219; попытка (вопрос) 2310; результат (ответ): один «бык» (цифра 1 из вопроса входит в тайное число и стоит на своем месте) и две «коровы» (цифры 2 и 3 из вопроса входят в тайное число, но стоят не на своем месте). Ответ сообщается в виде 2-значного числа. В нашем примере ответ – 12 (один «бык», две «коровы»). Игроки делают попытки по очереди. Побеждает тот, кто первым получит на свой вопрос ответ 40.

Скачать заметку в формате Word или pdf, примеры в формате Excel, пример Неоптимальный второй вопрос в формате zip (внутри Excel-файл на 57МВ).

Рекомендую скачивать после прочтения соответствующего места заметки, и только если поймете, что вам хочется изучить детали.

Вот какие идеи теории информации мне показались полезными для улучшения показателей в игре (см. Введение в теорию информации):

1. Вопрос нужно задавать так, чтобы ответ на него давал максимальное количество информации.
2. Для этого вопрос нужно формировать так, чтобы вероятности различных ответов были по возможности близкими.
3. Кроме того, вопрос должен быть таким, чтобы ответ на него не содержал информацию, полученную ранее из предыдущих вопросов.

Для лучшего понимания материала полезно также открыть Excel-файл.

1. Тайное число можно задумать 10*9*8*7 = 5040 способами (на первом месте может стоять любая из 10 цифр, на втором – любая из 9 оставшихся и т.д.). Для того, чтобы сформировать массив допустимых чисел я использовал простые алгоритмы в Excelе (см. листы «Подг1» и «Подг2»). Поскольку вероятность быть задуманным любого из 5040 чисел одинакова, неопределенность (Н) вычисляется по формуле Хартли: Н = log₂N. Перед началом игры неопределенность составляет log₂5040 = 12,30 бит информации.

2. Понятно, что первый вопрос может быть любым, например, 0123. На него возможны 14 ответов (см. также лист «Вопрос1» Excel-файла):

Ответ	Число ответов	р	H	h
00	360	7,1%	8,49	3,81
01	1440	28,6%	10,49	1,81
02	1260	25,0%	10,30	2,00
03	264	5,2%	8,04	4,25
04	9	0,2%	3,17	9,13
10	480	9,5%	8,91	3,39
11	720	14,3%	9,49	2,81
12	216	4,3%	7,75	4,54
13	8	0,2%	3,00	9,30
20	180	3,6%	7,49	4,81
21	72	1,4%	6,17	6,13
22	6	0,1%	2,58	9,71
30	24	0,5%	4,58	7,71
40	1	0,02%	0,00	12,30
	5040	100,0%	12,30	2,77

Здесь: р – вероятность ответа, Н – неопределенность, оставшаяся после соответствующего ответа, h – количество информации, полученное, если реализовался тот или иной ответ. Наиболее вероятный ответ – 01, означающий, что из вопроса в тайное число входит лишь одна цифра, причем стоит она не на своем месте. Ответ 01 подразумевает, что задуманным может быть одно из 1440 чисел, то есть неопределенность, оставшаяся после этого ответа, составляет log₂1440 = 10,49 бит, а информация, полученная при таком ответе 12,30 – 10,49 = 1,81 бит. Ответ 40 дает 12,30 бит информации, а неопределенности после него не остается J Поскольку вероятности ответов различны, количество информации, содержащееся в вопросе определяется по формуле Шеннона: Н(x) = p₁log₂(1/p₁) + p₂log₂(1/p₂) + … + p_Nlog₂(1/p_N). Первый вопрос приносит 2,77 бит информации.

3. При выборе второго вопроса следует руководствоваться тремя идеями сформулированными выше. На практике это означает, что вопрос должен допускать ответ 40.

Правило формирования второго вопроса. Пусть на первый вопрос (0123) мы получили ответ 01. Для второго вопроса возьмем одну цифру из первого вопроса, поставим ее на новое место и добавим три новые цифры. Получим, например, 4561. Если на вопрос1 был получен, например, ответ 11, надо взять две цифры из первого вопроса, одну оставить на своем месте, вторую поставить на новое место, и добавить две новые цифры; например, 0435.

На вопрос2 4561 также возможны 14 ответов (см. лист «Вопрос2»):

Ответ	Число ответов	р	H	h
00	54	3,8%	5,75	4,74
01	378	26,3%	8,56	1,93
02	369	25,6%	8,53	1,96
03	91	6,3%	6,51	3,98
04	6	0,4%	2,58	7,91
10	126	8,8%	6,98	3,51
11	222	15,4%	7,79	2,70
12	83	5,8%	6,38	4,12
13	6	0,4%	2,58	7,91
20	57	4,0%	5,83	4,66
21	31	2,2%	4,95	5,54
22	5	0,3%	2,32	8,17
30	11	0,8%	3,46	7,03
40	1	0,07%	0,00	10,49
	1440	100,0%	10,49	2,86

Выбранный нами второй вопрос принес 2,86 бита информации. Посмотрим, сколько информации дадут другие вторые вопросы. Для этих целей я создал отдельный файл «Неоптимальный второй вопрос.xlsx» (он «весит» 58МВ, поэтому будьте с ним аккуратнее :)). Второй вопрос может быть одним из 5040 возможных чисел (в том числе и повторение первого вопроса). В итоге этого исследования я получил количество информации, которое дают те или иные вторые вопросы (напомню, что анализ сделан в предположении, что первый вопрос 0123 дал ответ 01). Например, вопрос2 – 0123 дает ноль битов информации, так как на него возможен только один ответ 01, а (для N = 1) log₂1 = 0. Вопрос2 0132 дает 0,65 бит информации, вопрос2 0148 – 2,53 бита информации. Максимальное количество информации дают 1440 вторых вопросов, сформированных по выше описанному правилу. Результаты исследования я перенес на лист «Разные вопросы2» файла «Быки-коровы.xlsx» и далее буду говорить только об этом файле.

Как я уже сказал, максимальное количество информации – 2,859 – будет получено на вопрос2, подготовленный следующим образом: надо взять одну цифру из первого вопроса, поставить ее на новое место и добавить три новые цифры:

Информация от вопроса2, бит	Число таких вопросов
0,000	1
0,650	6
0,811	8
0,918	9
1,899	24
2,104	72
2,258	144
2,268	72
2,365	216
2,372	48
2,530	180
2,624	360
2,664	720
2,756	360
2,766	480
2,767	720
2,774	180
2,859	1440
Итого	5040

Видно, что еще 180 вопросов дают почти столько же информации – 2,774 бита. Такое количество информации будет получено при ответе, например, на вопрос 1045 (см. лист «Вопрос2неопт»). Но этот вопрос не может дать ответа 40! То есть, вопрос подготовлен с нарушением сформулированного правила. Насколько велика разница в информации между 2,859 и 2,774 бита!? На первый взгляд она не выглядит большой. С другой стороны, при самом неблагоприятном ответе на вопрос2 4561 (01) останется 378 вариантов тайного числа, а при самом неблагоприятном ответе на вопрос2 1045 (также 01) – 408 вариантов. На 8% больше! Это и есть цена неоптимального вопроса.

4. При подготовке третьего (и последующих) вопросов я руководствуюсь следующим мнемоническим правилом. Необходимо составить агрегированную таблицу всех возможных тайных чисел, удовлетворяющих ответам на предыдущие вопросы. После этого сформировать вопрос3, используя ту часть этой таблицы, которая содержит больше вариантов (оценку произвожу «на глазок»). Немного запутанно? Давайте рассмотрим два примера.

Пример1. Первые два вопроса и ответа были следующими:

Вопрос1	0123		Ответ1	01
Вопрос2	4561		Ответ2	01

Первый вариант: входит единица, тогда не входят, ни 023, ни 456; то есть входят, не использовавшиеся в первых двух вопросах, цифры – 789. Получаем набор цифр тайного числа 1789 (порядок их расположения любой, удовлетворяющий ответам на первые два вопроса). Вариантов, отвечающих этому набору, 12.

Второй вариант: единица не входит, тогда входит одна цифра из 023, одна – из 456, и две – из 789. Записываю я это так:

Ориентировочное число вариантов набора цифр равняется 3 (одна из 023) * 3 (одна из 456) * 3 (две из 789) = 27. А с учетом мест расположения цифр вариантов существенно более 100. Для вопроса3 берем одну цифру из 023, одну из 456, две из 789. Располагаем цифры так, чтобы не было совпадений мест расположения с вопросом1 и вопросом2. Более того, располагаем цифры, которые ранее уже встречались (4 и 2) на совершенно новых местах, то есть на 2-м или 4-м. Например, вопрос3 7482 лучше, чем 2784. Так как в первом случае 4-ка и 2-ка стоят на местах, которые в вопросе1 и вопрос2 они не занимали. В то же время, в вопросе3 2784 цифра 2 стоит на месте 4-ки из вопроса2 (см. лист «Вопрос3»). Ответ на вопрос3 4782 содержит 2,958 бит информации, а ответ на вопрос 3 2784 – «только» 2,955.

Пример2. Первые два вопроса и ответа были следующими:

Вопрос1	0123		Ответ1	02
Вопрос2	3541		Ответ2	02

Первый вариант: входят 13, тогда не входят, ни 02, ни 45, а из оставшихся цифр входят две:

Количество тайных числе в варианте1 – 48.

Второй вариант: входит одна цифра из 13, тогда входит одна – из 02, одна – из 45, и одна – из 6789:

Ориентировочное количество тайных чисел в варианте2 – более 100.

Третий вариант: не входят 13, тогда входят и 02, и 45: 0245. Количество тайных чисел в варианте3 – 8.

Итак для вопроса3 выбираем число из варианта2, например, 1705.

5. Когда тайных чисел остается мало (от 4 до 10…20), я перехожу на полный перебор всех возможных вариантов.

Играйте с алгоритмом, построенным на основе теории информации, и выигрывайте!

Дополнение от 14 февраля 2015 г.

Нурым Кенжебеков написал программу, позволяющую играть с компьютером. Программа работает под Windows 7, 8, 8.1 с установленным Framework 4.5. Игра мне очень понравилась, но алгоритм явно далек от оптимального. Я сыграл трижды и все три раза выиграл.

Скачать программу в формате архива.

---

[1] http://slovesnov.narod.ru/articles/bullcow.pdf. Сказать по правде, мне не удалось ее осилить 🙂 Но упоминаний теории информации при беглом просмотре я в ней не нашел…

baguzin.ru

Быки и коровы — это… Что такое Быки и коровы?

Быки и коровы — логическая игра для двоих игроков. Для игры достаточно иметь бумагу, ручку и уметь считать. Также игра может называться «цифры» или «цвета».

Правила игры

Играют двое. Каждый задумывает и записывает тайное 4-значное число с неповторяющимися цифрами^[1]. Игрок, который начинает игру по жребию, делает попытку отгадать число. Попытка — это 4-значное число с неповторяющимися цифрами, сообщаемое противнику. Противник сообщает в ответ, сколько цифр угадано без совпадения с их позициями в тайном числе и сколько угадано вплоть до позиции в тайном числе. Например:

Задумано тайное число «3219».

Попытка номер: «2310».

Результат: две «коровы» (две цифры: «2» и «3» — угаданы на неверных позициях) и один «бык» (одна цифра «1» угадана вплоть до позиции).

Игроки делают попытки угадать по очереди. Побеждает тот, кто угадает число первым.

Вариации игры

В игре «мастермайнд» (англ. Mastermind, возможный перевод: «гениальный отгадчик») загадывается последовательность из 4 цветных фишек, причём цвета могут повторяться.

В усложнённом варианте может использоваться последовательность из 5, 6 или большего количества фишек^{[2][3][неавторитетный источник? 661 день]}.

Существует вариант^{[неавторитетный источник? 661 день]} игры со словами. То есть игрок загадывает слово, обычно из 5 букв (в именительном падеже единственном числе по правилам игры «балда»), и задача противника — угадать его, используя в качестве попыток такие же корректные слова из словаря русского языка.

Алгоритм

В общем случае количество вариантов для k-значного числа в N-ричной системе счисления без повторений, будет равно числу размещений: .

В случае варианта с повторениями количество вариантов будет равно .

Большинство известных алгоритмов суть вариации алгоритма полного перебора с определённой эвристикой^[4]. В связи с тем, что количество вариантов не столь велико и схема прямого перебора элементарно реализуется, компьютер играет в «быки и коровы» намного сильнее человека. Чем больше знаков в числе, тем больше разница в силе игры человека и компьютера.

Настольный вариант игры Mastermind для 4 мест и 6 цветов

Как показал Дональд Кнут, для игры Mastermind (6⁴ вариантов) при предложенной им стратегии нужно не более 5 попыток, чтобы отгадать любую комбинацию, и в среднем 4,34 попыток для отгадывания^[5].

В классическом случае игры с четырьмя не повторяющимися цифрами для отгадывания любого номера требуется не более семи ходов. Средняя минимальная длина игры составляет 26274/5040=5.2131 попытки^[6].

Реализации

Существует множество вариантов компьютерной реализации игры, в том числе для мобильных телефонов и мобильных компьютеров.

Настольные игры Mastermind популярны во всём мире. Наиболее распространены вариации:

• классическая, четыре не повторяющиеся цифры.
• обычная, 4 места для фишек 6 цветов с повторениями.
• продвинутая, 5 мест для фишек 8 цветов^{[источник не указан 224 дня]}.

Ссылки

• Кандидат технических наук Е. Гик. Быки и коровы. «Наука и жизнь», № 2, 1978, с. 150—151; № 8, 1978, с. 142—143.
• Чарльз Уэзерелл. Этюды по программированию, Великий комбинатор. М.: 1982, с. 140.

Примечания

dic.academic.ru

Быки и коровы решение

Приветствую Вас, уважаемые любители логических игр. Сейчас я хочу поделиться с Вами примером игры и решением задачи быки и коровы. В другой статье я описал общие концепции и немного теории. Но в ней проблема изложена несколько поверхностно. Теперь же рассмотрим досконально, как и что надо делать.

И так, первый ход он всегда на удачу. Выбираем любые четыре цифры. К примеру 1234.

Получаем ответ две коровы. Что это нам даёт? Мы нашли две цифры, но не знаем какие они и где должны стоят. Не будем пока их трогать и пытаться выяснить кто есть кто. Это будет напрасной тратой драгоценных ходов. Идём дальше и второй вопрос составляем из других цифр. К примеру, 5678.

Мы получили в ответ один бык и одну корову. Хочу сказать, что мы тут молодцы и удача нам улыбается. Нам удалось выявить, что ноль и девять не состоят в загаданном числе. И теперь мы их можем использовать для определения быков! Таким образом у нас с Вами есть два варианта развития дальнейших событий. Это искать быков из первого или второго вопроса. Я выберу первый, так как в этом варианте нет быков и все цифры не на своих местах. Снова скрестим пальцы на удачу. Выберем две цифры и переставим их местами, думаю взять 3 и 4, и поставить их на первое и второе место. И добьём третий вопрос нашими пустышками 0 и 9. Получаем такой вопрос 3490.

Ответ просто волшебный! Два быка. Мы снова угадали 3 и 4 — это и есть быки. Значит единичка и двойка вне игры. Осталось найти вторую пару цифр. Начинаем перебирать цифры с нашего второго вопроса. Возьмём 5 и 7, но поставим их на другие места. Это важный момент — места нужно менять, у нас ведь во втором ответе имеется один бык и есть шанс 25%, что мы этого быка снова поставим на место в третьем вопросе и у нас будет неоднозначность, какая из второй пары цифр точно есть бык. И таким образом получаем четвёртый вопрос — 3457.

Пришёл ответ — два быка и одна корова. Два быка это наши угаданные с третьей попытки 3 и 4. Корова — это одна их цифр 5 или 7. Но мы можем точно определить быка, у нас ведь во втором ответе есть один бык. Пятёрка чтобы быть быком должна стоять на первом месте, а это место у нас занято тройкой. Значит остаётся цифра семь и должна она стоять на третьем месте!

Продолжаем рассуждать дальше. У нас осталось две цифры — шесть и восемь. Что нам о них известно? А то, что во втором ответе одна из них является коровой, то есть стоит не на своём месте. Шестёрка на втором, восьмёрка на четвёртом. У нас свободно осталось только четвёртое место! И если это 8, то у нас возникнет противоречие, так как тогда во втором ответе она должна была быть быком, потому что стоит на четвёртом месте! В ходе таких рассуждений мы абсолютно точно выявили, что цифра шесть это наш четвёртый бык и стоит она на четвёртой позиции. Проверяем: 3476.

И Чудеса! Четыре быка. Поздравляю мы победили!

Здесь рассмотрен вариант решения одиночной игры быки и коровы против компьютера, в который можно сыграть у нас на сайте. Но при игре онлайн против живого противника принцип разгадывания числа ничем не отличается. И я надеюсь, что я Вам помог немного разобраться в принципах игры.

Пожелания, критику или Ваши предложения жду на форуме или на почту.

xn--90aeltibbl.xn--p1ai

Быки и коровы Википедия

Быки и коровы
Скриншот компьютерной версии игры. Партия выиграна за семь ходов
Игроков	2
Длительность партии	5-30 минут
Сложность правил	Низкая
Уровень стратегии	Низкая
Влияние случайности	Низкое
Развивает навыки	логичность мышления, счёт, память

Быки и коровы — логическая игра, в ходе которой за несколько попыток один из игроков должен определить, что задумал другой игрок. Варианты игры могут зависеть от типа отгадываемой последовательности — это могут быть числа, цвета, пиктограммы или слова. После каждой попытки задумавший игрок выставляет «оценку», указывая количество угаданного без совпадения с их позициями (количество «коров») и полных совпадений (количество «быков»). Роли участников игры не равнозначны — угадывающий должен анализировать сделанные попытки и полученные оценки, то есть его роль активна. Его партнёр лишь сравнивает очередной вариант с задуманным и выставляет оценку по формальным правилам, то есть его роль пассивна. Для уравновешивания ролей одновременно играют две встречные партии.

Первоначально игра была задумана для двух игроков, но с появлением компьютерных версий стал популярен вариант, когда игрок отгадывает число, задуманное программой, то есть играет в одиночку. Для игры вдвоем достаточно иметь бумагу и ручку. В электронных версиях игру на расстоянии против противника обеспечивает функция многопользовательской игры (multiplayer).

Правила игры[ | ]

В классическом варианте игра рассчитана на двух игроков. Каждый из игроков задумывает и записывает тайное 4-значное число с неповторяющимися цифрами^[1]. Игрок, который начинает игру по жребию, делает первую попытку отгадать число. Попытка — это 4-значное число с неповторяющимися цифрами, сообщаемое противнику. Противник сообщает в ответ, сколько цифр угадано без совпадения с их позициями в тайном числе (то есть количество коров) и сколько угадано вплоть до позиции в тайном числе (то есть количество быков). Например:

Задумано тайное число «3219».

Попытка: «2310».

Результат: две «коровы» (две цифры: «2» и «3» — угаданы на неверных позициях) и один «бык» (одна цифра «1» угадана вплоть до позиции).

Игроки делают попытки угадать по очереди. Побеждает тот, кто угадает число первым, при условии, что он не начинал игру. Если же отгадавший начинал игру — его противнику предоставляется последний шанс угадать последовательность.

При игре против компьютера игрок вводит комбинации одну за другой, пока не отгадает всю последовательность.

Вариации игры[ | ]

В игре «мастермайнд» (англ. Mastermind, возможный перевод: «Интеллектуал, умник») загадывается последовательность из 4 цветных фишек, причём цвета могут повторяться. В усложнённом варианте может использоваться последовательность из 5, 6 или большего количества фишек^[2]

Существует вариант игры со словами^{[источник не указан 2109 дней]}. То есть игрок загадывает слово, обычно из 5 букв (в именительном падеже единственном числе по правилам игры «балда»), и задача противника — угадать его, используя в качестве попыток такие же корректные слова из словаря русского языка. Однако, существует и вариант, когда возможно использование произвольного сочетания букв.

Алгоритм[ | ]

В общем случае количество вариантов для k-значного числа в N-ричной системе счисления без повторений, будет равно числу размещений: ANk=N!(N−k)!{\displaystyle A_{N}^{k}={\frac {N!}{(N-k)!}}}.

В случае варианта с повторениями количество вариантов будет равно Nk

ru-wiki.ru